A、β<sub>1</sub>=α<sub>1</sub>-α<sub>2</sub>-α<sub>3</sub>,β<sub>2</sub>=α<sub>1</sub>+α<sub>2</sub>-α<sub>3</sub>,β<sub>3</sub>=-α<sub>1</sub>+α<sub>2</sub>+α<sub>3</sub>,向量组β<sub>1</sub>,β<sub>2</sub>,β<sub>3</sub>线性无关
B、β<sub>1</sub>=α<sub>1</sub>-α<sub>2</sub>+α<sub>3</sub>,β<sub>2</sub>=α<sub>2</sub>-α<sub>3</sub>,β<sub>3</sub>=α<sub>3</sub>-α<sub>1</sub>,向量组β<sub>1</sub>,β<sub>2</sub>,β<sub>3</sub>线性相关
C、β<sub>1</sub>=α<sub>1</sub>+α<sub>2</sub>,β<sub>2</sub>=α<sub>2</sub>-α<sub>3</sub>,β<sub>3</sub>=α<sub>3</sub>+α<sub>1</sub>,向量组β<sub>1</sub>,β<sub>2</sub>,β<sub>3</sub>线性无关
D、β<sub>1</sub>=α<sub>1</sub>-α<sub>2</sub>+α<sub>3</sub>,β<sub>2</sub>=-α<sub>1</sub>+α<sub>3</sub>,β<sub>3</sub>=-α<sub>1</sub>+2α<sub>2</sub>+α<sub>3</sub>,向量组β<sub>1</sub>,β<sub>2</sub>,β<sub>3</sub>线
查看答案
正确答案
试题解析
[解析] (β
1,β
2,β
3)=(α
1,α
2,α
3)A,由于α
1,α
2,α
3线性无关,因此,向量组β
1,β
2,β
3线性无关的充分必要条件是|A|=0。
选项A中的

,向量组β
1,β
2,β
3线性相关,故选项A不正确;
选项B中的
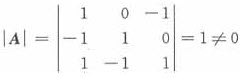
,向量组β
1,β
2,β
3线性无关,故选项B不正确;
选项C中的
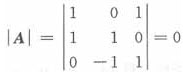
,向量组β
1,β
2,β
3线性相关,故选项C不正确;
选项D中的
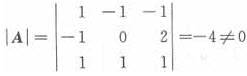
,向量组β
1,β
2,β
3线性无关,故正确答案为D。
