不考虑杆件的轴向变形,下图所示体系的振动自由度为( )。

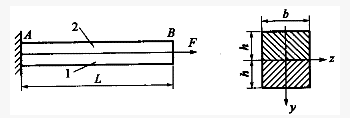
(2013)两根杆粘合在一起,截面尺寸如图。杆1的弹性模量为E1,杆2的弹性模量为Ez,且E1=2E2。若轴向力F作用在截面形心,则杆件发生的变形是:()
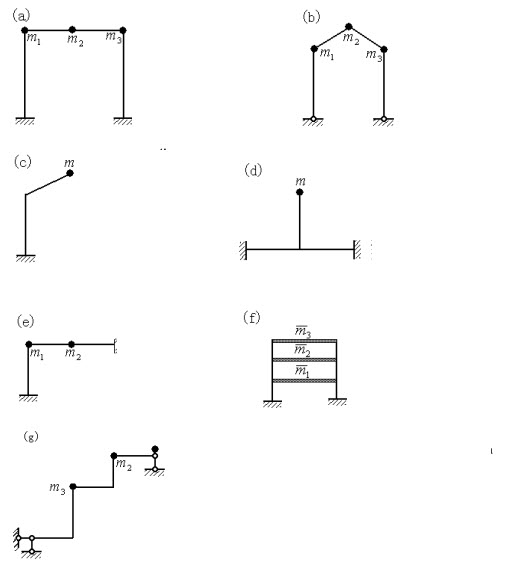
图示三种单自由度动力体系中,质量m均在杆件中点,各杆EI、l相同。其自振频率的大小排列次序为:()
设直杆的轴向变形不计,图示体系的动力自由度数为:()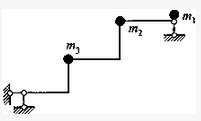
设直杆的轴向变形不计,图示体系的动力自由度数为:()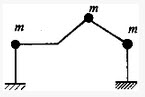



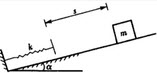
如图所示,在倾角为α的光滑斜面上置一刚性系数为k的弹簧,一质量为m的物体沿斜面下滑s距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率为()。
下图所示的网络搭接关系为()。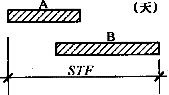

体系的实际自由度绝对不小于其计算自由度。
如果在一个体系中增加一个约束,而体系的自由度并不因此减少,则称此约束为多余约束。
忽略直杆轴向变形的影响,图示体系有振动自由度为( )。

单自由度体系的自由振动主要计算( )
在超静定结构计算中,一部分杆考虑弯曲变形,另一部分杆考虑轴向变形,则此结构为
在结构动力计算中,四质点的振动体系,其振动自由度一定为4。
不考虑杆件的轴向变形,下图所示体系的振动自由度为( )。

4.下图所示平面杆件体系是何种杆件体系( )
\/img/1-1-4.png)
图示振动体系的自由度数目为( )

图示体系有1个振动自由度。

不考虑杆件的轴向变形,下图所示体系的振动自由度为( )。

不考虑杆件的轴向变形,下图所示体系的振动自由度为( )。

图示体系有1个振动自由度。

图示振动体系的自由度数目为( )

图示振动体系的自由度数目为( )

图示振动体系的自由度数目为( )


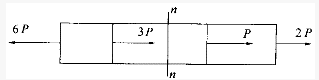
如图所示受力杆件中,n—n截面上的轴力为:()
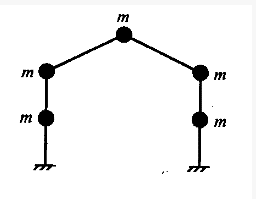
若忽略杆件的轴向变形,图示体系的动力自由度数为()。
槽钢梁一端固定,一端自由,自由端受集中力P作用,梁的横截面和力P作用线如图所示(C点为横截面形心),其变形状态为:()

免费的网站请分享给朋友吧