设图G是有5个结点的连通图，结点度数总和为10，则可从G中删去6条边后使之变成树．( )
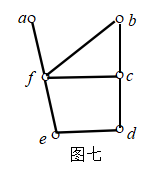
设图G如图七所示，则图G的点割集是{f}．( )
如果图G是无向图，且其结点度数均为偶数，则图G存在一条欧拉回路．( )
设P：他生病了，Q：他出差了，R：我同意他不参加学习．那么命题“如果他生病或出差了，我就同意他不参加学习”符号化的结果为(P∨Q)→┐R．( )
命题公式┐P∧(P∨Q)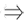
Q成立． ( )
命题公式┐(P→Q)的主析取范式是P∨┐Q．( )
命题公式┐P∧P的真值是T．( )
设P：昨天下雨，Q：今天下雨．那么命题“昨天下雨，今天仍然下雨”符号化的结果为P∧Q．( )
含有三个命题变项P，Q，R的命题公式P∧Q的主析取范式(P∧Q∧R)∨(P∧Q∧┐R)．( )
命题公式P→(Q∨P)的真值是T．( )
命题公式┐P∧(P→┐Q)∨P为永真式．( )
设P：小王来学校， Q：他会参加比赛．那么命题“如果小王来学校，则他会参加比赛”符号化的结果为P→Q．( )
设P：我们下午2点去礼堂看电影，Q：我们下午2点去教室看书．那么命题“我们下午2点或者去礼堂看电影或者去教室看书” 符号化的结果为P∨Q．( )
（3.1）A支座的水平方向支座反力FAx=（ ）（2分）
（1.1）B支座的支座反力FRB =（ ）（4分）
（1.3）A支座的竖直方向支座反力FAy=（ ）（2分）
（4.1）B 支座的支座反力FRB =（ ）（4分）
（5.1）D支座的支座反力FRD =（ ）（2分）
（2.1）B支座的支座反力FRB =（ ）（4分）
若集合A = {1，2，3}上的二元关系R={<1, 1>，<1, 2>，<3, 3>}，则R是对称的关系．（ ）
设集合A={1, 2, 3}，B={2, 3, 4}，C={3, 4, 5}，则A∩(C-B )= {1, 2, 3, 5}．（ ）
设A={1，2，3 }，R={<1，1 >, <1，2 >，<2，1 >, <3，3 >}，则R是等价关系．（ ）
设R是集合A上的等价关系，且1 , 2 , 3是A中的元素，则R中至少包含<1, 1>，<2, 2>，<3, 3> 等元素．（ ）
设A={2, 3}，B={1, 2}，C={3, 4}，从A到B的函数f={<2, 2>, <3, 1>}，从B到C的函数g={<1，3>, <2，4>}，则Dom(g° f) ={2，3}．（ ）
设G是一个有7个结点16条边的连通图，则G为平面图．( )
设连通平面图G的结点数为5，边数为6，则面数为4．( )
设G是一个连通平面图，且有6个结点11条边，则G有7个面．( )
无向图G存在欧拉回路，当且仅当G连通且结点度数都是偶数．( )
结点数v与边数e满足e=v的无向连通图就是树．( )
无向图G的结点数比边数多1，则G是树．( )
设图G是有6个结点的连通图，结点的总度数为18，则可从G中删去4条边后使之变成树．( )
已知图G中有1个1度结点，2个2度结点，3个3度结点，4个4度结点，则G的边数是15．( )
设图G是有5个结点的连通图，结点度数总和为10，则可从G中删去6条边后使之变成树．( )
免费的网站请分享给朋友吧