阳极旋转速度的公式是n=(120f/P)·(1-s),式中P的取值是
设f(x)=5x^4-2x^3 |x|,则使f^(n) (0)存在的最大n值是( )。

设函数f:N→N,f(n)=n+1,下列表述正确的是( ).
小球动能减小一半,速度从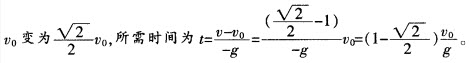 F1、F2是力F的两个分力。若F=10N,则下列不可能是F的两个分力的是()
F1、F2是力F的两个分力。若F=10N,则下列不可能是F的两个分力的是()
现值的计算公式为:P=S×(1+R)n
设数列{an}前n项和为Sn,且an+Sn=1(n∈N*)
(1)求{an}的通项公式;
(2)若数列{bn}满足b1=1且2bn+1=bn+an(n≥1),求数列{bn}的通项公式。
免费的网站请分享给朋友吧