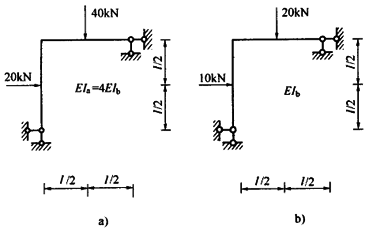
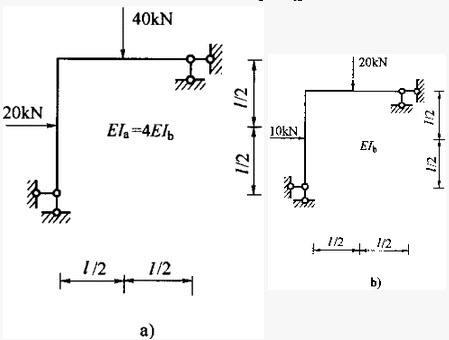
图示两刚架的EI均为常数，已知EI_a=4EI_b2，则图a）刚架各截面弯矩为图b）刚架各相应截面弯矩的倍数关系为：（）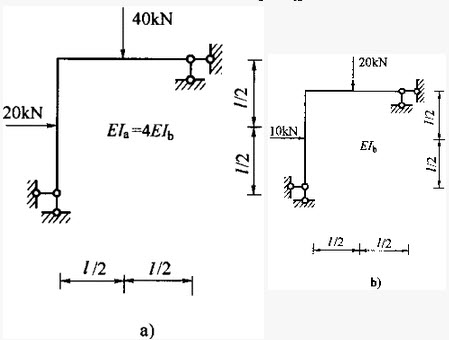

同一结构，不考虑阻尼时的自振频率为ω，考虑阻尼时的自振频率为ω_D，则（  　）

同一结构，不考虑阻尼时的自振频率为ω，考虑阻尼时的自振频率为ω_D，则（  　）

盛水容器a和b的上方密封，测压管水面位置如图所示，其底部压强分别为p_a和p_b。若两容器内水深相等，则p_a和p_b的关系为：（）

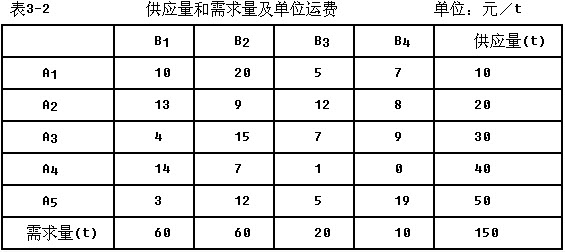
设有5个产地A₁、A₂、A₃、A₄、A₅和4个销地B₁、B₂、B₃、B₄的运输问题，它们的供应量和需求量及单位运费见表3-2。试计算其最小运输成本。

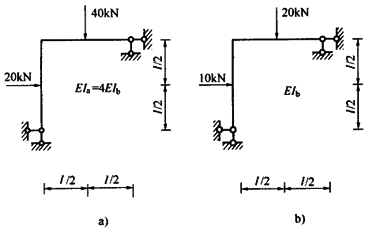
图示两刚架的EI均为常数，已知EI_a=4EI_b，则图a）刚架各截面弯矩与图b）刚架各相应截面弯矩的倍数关系为：（）

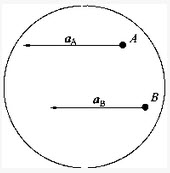
图示瞬时，作平面运动图形上A、B两点的加速度相等，即a_A=a_b，则该瞬时平面图形的角速度ω与角加速度a分别是：（）

两红线桩A、B的坐标分别为x_A=1000．000m、y_A=2000．000m，x_b=1060．000m、y_b=2080．000m；欲测设建筑物上的一点M，x_m=991．000m、y_m=2090．000m。则在A点以B点为后视点，用极坐标法测设M点的极距D_AM和极角∠BAM分别为：（）

设数列｛a_n｝前n项和为S_n，且a_n+S_n=1（n∈N^*）
（1）求｛a_n｝的通项公式；
（2）若数列｛b_n｝满足b₁=1且2b_n+1=b_n+a_n（n≥1），求数列｛b_n｝的通项公式。