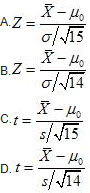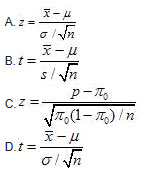设总体为正态总体，总体方差未知，在小样本条件下，对总体均值进行如下的假设检验H0：μ=μ0，（μ0为已知数）；Hl：μ≠μ0，α=0.1。则下列说法正确的有（　　）。 -题库考试答案搜索网

设总体为正态总体，总体方差未知，在小样本条件下，对总体均值进行如下的假设检验H0：μ=μ0，（μ0为已知数）；Hl：μ≠μ0，α=0.1。则下列说法正确的有（　　）。

多选题

2022-10-01 02:46

A、（-∞，-z<sub>0.10</sub>）和（z<sub>0.10</sub>，+∞）为原假设的拒绝区域
B、（-∞，-z<sub>0.05</sub>）和（z<sub>0.05</sub>，+∞）为原假设的拒绝区域
C、（-∞，-t<sub>0.10</sub>）和（t<sub>0.10</sub>，+∞）为原假设的拒绝区域
D、（-∞，-t<sub>0.05</sub>）和（t<sub>0.05</sub>，+∞）为原假设的拒绝区域
E、若检验统计量的绝对值越大，则原假设越容易被拒绝

查看答案

正确答案

D | E

试题解析

总体为正态总体，总体方差未知时，构造t统计量：

，当|t|＞t_α/2（n-1）时，拒绝原假设。本题中原假设的拒绝区域为（-∞，-t_0.05）和（t_0.05，+∞），检验统计量的绝对值越大，|t|＞t_α/2（n-1）越容易成立，原假设越容易被拒绝。

标签：中级统计师统计基础理论及相关知识

感兴趣题目

当样本是小样本，总体服从正态分布，总体方差未知而要进行小样本与总体间某个统计量的差异显著性检验，常采用（）。

大样本情况下，当总体方差未知时，总体均值检验的统计量为（　　）。

小样本情况下，当总体服从正态分布，总体方差已知时，总体均值检验的统计量为（　　）。

小样本情况下，总体服从正态分布，总体方差未知，总体均值在置信水平（1-α）下的置信区间为（）

小样本情况下，总体服从正态分布，总体方差未知，总体均值在置信水平（1-α）下的置信区间为（　　）。

假设检验中，在小样本的情况下，如果总体不服从正态分布，且总体方差未知，则经过标准化的样本均值服从（）

设总体服从正态分布，方差未知，在样本容量和置信度保持不变的情形下，根据不同的样本值得到总体均值的置信区间长度将（）。

设总体为正态总体，总体方差未知，在小样本条件下，对总体均值进行如下的假设检验H0：μ=μ0，（μ0为已知数）；Hl：μ≠μ0，α=0.1。则下列说法正确的有（　　）。

从一个正态分布总体中抽取样本，在总体方差已知时样本的平均数和方差分别服从（）分布和（）分布；在总体方差未知时样本的平均数服从（）分布。从两个正态分布总体中抽取样本，在总体方差已知和未知时样本平均数的差分别服从（）分布和（）分布。

原总体为正态，总体方差未知且样本容量小于30情况下的平均数抽样分布为（）

当正态总体的方差未知，且为大样本条件下，估计总体均值使用的分布是（）

设总体服从正态分布，总体方差未知，现抽取一容量为15的样本，拟对总体均值进行假设检验，检验统计量是（　　）。

相关题目: 小样本情况下，总体服从正态分布，总体方差未知，总体均值在置信水平（1-α）下的置信区间为（　　）。; 当正态总体的方差未知，且为小样本条件下，构造总体均值的置信区间使用的分布是（　　）。; 当正态总体方差已知时，在小样本情况下可以用正态分布对总体均值进行估计。（　　）; 当总体为正态总体，方差已知，样本量为40，此时进行均值检验，应采用( )统计量进行检验。; 设总体服从正态分布，总体方差未知，现抽取一容量为15的样本，拟对总体均值进行假设检验，检验统计量是（）。; 小样本情况下，当总体服从正态分布，总体方差未知时，总体均值检验的统计量为（）。; 当正态总体方差已知时，在小样本情况下可以用正态分布对总体均值进行估计。（）; 原总体为正态，总体方差未知且样本容量小于30情况下的平均数抽样分布为（）; 设总体X～N（μ，σ2），X1，X2，X3，X4是正态总体X的一个样本，为样本均值，S2为样本方差，若μ为未知参数且σ为已知参数，下列随机变量中属于统计量的有（）。; 设总体X～N(μ，σ2)，X1，X2，X3，X4是正态总体X的一个样本，为样本均值，S2为样本方差，若μ为未知参数且σ为已知参数，下列随机变量中属于统计量的有( )。; 设总体为正态总体，总体方差未知，在小样本条件下，对总体均值进行如下的假设检验H0：μ=μ0，（μ0为已知数）；Hl：μ≠μ0，α=0.1。则下列说法正确的有（）。; 设总体为正态总体，总体方差未知，在小样本条件下，对总体均值进行如下的假设检验H0：μ=μ0，（μ0为已知数）；Hl：μ≠μ0，α=0.1。则下列说法正确的有（　　）。; 当正态总体的方差未知时，且为小样本条件下，估计总体均值使用的分布是（）; 设总体服从正态分布，总体方差未知，现抽取一容量为15的样本，拟对总体均值进行假设检验，检验统计量是（　　）。; 当正态总体的方差未知，且为小样本条件下，构造总体均值的置信区间使用的分布是（）。; 当正态总体的方差未知，且为小样本条件下，构造总体均值的置信区间使用的分布是（　　）。; 大样本情况下，当总体方差未知时，总体均值检验的统计量为（　　）。; 当总体为正态总体，方差已知，样本量为40，此时进行均值检验，应采用（）统计量进行检验。; 当所检验的差异服从或近似于正态分布、总体方差未知，小样本统计量的差异显著性可采用（）。; 在小样本的总体均值检验中，如果总体方差σ 2 未知，则应采用（）。

广告位招租WX:84302438

题库考试答案搜索网

免费的网站请分享给朋友吧