图5-8-6所示线弹性材料简支梁AB，承受均布载荷q，集中力P，集中力偶M作用，挠曲线如图示。设U为梁的应变能，则 
的几何意义为：（） 
的几何意义为：（）
图示简支梁受均布荷载g及集中力偶m作用，则梁内的最大弯矩为（）。
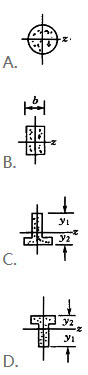
矩形截面简支梁梁中点承受集中力F。若h＝2b，分别采用图a图b两种方式放置，图a梁的最大挠度是图b梁的：（）
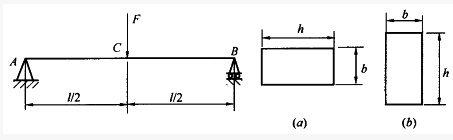
（2011）矩形截面简支梁中点承受集中力F。若h=2b，分别采用图a）、图b）两种方式放置，图a）梁的最大挠度是图b）梁的：（）
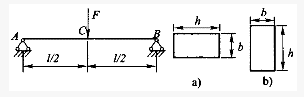
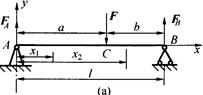
计算题：图a所示简支梁AB，在C点受集中力F作用，列出弯矩方程，并画出弯矩图。
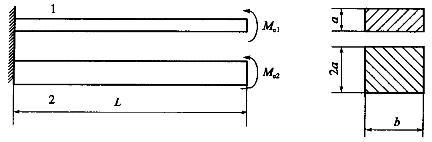
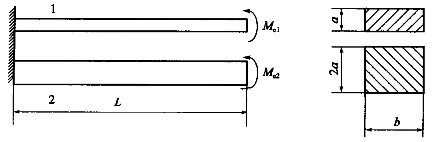
两根矩形截面悬臂梁，弹性模量均为E，横截面尺寸如图，两梁的载荷均为作用在自由端的集中力偶。已知两梁的最大挠度相同，则集中力偶Me2是Me1的：（）（悬臂梁受自由端集中力偶M作用，自由端挠度为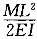
）
梁AB一端固定、一端自由，如图所示。梁上作用有均布载荷，载荷集度为q=10kN／m。在梁的自由端还受有集中力F=30kN和力偶矩为M=10kN·m作用，梁的长度为L=1m，试求固定端A处的约束反力。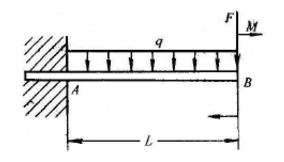
） 
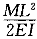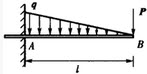
免费的网站请分享给朋友吧