点作直线运动，已知某瞬时加速度a=-2m/s2，t=1s时速度为铆，=2m/s，则t=2s时，该点的速度大小为() -题库考试答案搜索网

点作直线运动，已知某瞬时加速度a=-2m/s2，t=1s时速度为铆，=2m/s，则t=2s时，该点的速度大小为()

单选题

2021-07-17 17:33

B、-2m/s
C、4m/s
D、无法确定

查看答案

正确答案

D

试题解析

标签：第四章理论力学岩土工程基础知识

感兴趣题目

在某瞬时一动点的法向加速度等于零，而其切向加速度不等于零，该点是作直线运动还是作曲线运动？（）

点作直线运动，已知某瞬时加速度a=-2m/s2，t=1s时速度为v1=2m/s，则t=2s时，该点的速度大小为：（）

一物体做变速直线运动，它的速度函数是v=2t+1，t=1时该物体的瞬时加速度为（）。

（2005）已知点作直线运动，其运动方程为x=12-t3（x以cm计，t以秒计）。则点在前3秒钟内走过的路程为：（）

已知一动点作圆周运动，且其法向加速度越来越大，则该点运动的速度（）。

一物体做变速直线运动，它的位置函数是s=，t=2时该物体的瞬时速度为4。

下述各种情况下，动点的全加速度a、切向加速度a_t和法向加速度a_n三个矢量之间正确的是（）。
（1）点沿曲线作匀速运动。
（2）点沿曲线运动，在该瞬时其速度为零。
（3）点沿直线作变速运动。
（4）点沿曲线作变速运动。

曲柄连杆机构在运动的过程中，当达到某位置时，滑块的瞬时运动速度为零。此时的位置是（）。

一动点作平面曲线运动，若其速率不变，则其速度矢量与加速度矢量（）.

下述各种情况下，动点的全加速度a、切向加速度at和法向加速度an三个矢量之间正确的是（）。（1）点沿曲线作匀速运动。（2）点沿曲线运动，在该瞬时其速度为零。（3）点沿直线作变速运动。（4）点沿曲线作变速运动。

在任一瞬时，平动运动物体的绝对加速度等于运动物体的牵连加速度与相对加速度的矢量和。

一、教材阅读 1、平均速度与瞬时速度的区别与联系 (1)平均速度是运动物体在某一段时间内位移的平均值,即用时间除位移得到,(2)瞬时速度是物体在某一时间点的速度, 当时间段越来越的过程中,平均速度就越来越接近一个数值,这个数值就是瞬时速度, 可以说,瞬时速度是平均速度在时间间隔无限趋于时的 “飞跃”. 2 、求瞬时速度的步骤设物体运动方程为 s = f ( t ) , 则求物体在 t 时刻瞬时速度的步骤为: (1) 从 t 到 t + d 这段时间内的平均速度为 d ( f(t+d)-f(t) ) , 其中 f ( t + d ) - f ( t ) 称为位移的增量; (2) 对上式化简 , 并令 d 趋于 , 得到极限数值即为物体在 t 时刻的瞬速度. 3、曲线的割线与切线的区别与联系 (1) 曲线的割线的斜率反映了曲线在这一区上上升或下降的变化趋势 ,刻画了曲线在这一区间升降的程度, (2)曲线的切线是割线与曲线的一交点向另一交点逼时的一种极限状态,它实现了由割线向切线质的飞跃. 4、求曲线上点 P 处切线斜率的方法设 P ( u , f ( u )) 是函数 y = f ( x ) 的曲线上的任一点,则求点 P 处切线斜率的方法是: (1) 在曲线上取不同于 P 的点 Q ( u + d , f ( u + d )) , 计算直线 PQ 的斜率 k ( u , d ) = . (2) 在所求得的 PQ 的斜率的表达式 k ( u , d ) 中让 d 趋于 0 , 如果 k ( u , d ) 趋于确的数值 k ( u ) ,则就是曲线在 P 处的切线斜率. 二、基础作业: 1、已知一物体作自由落体运动 , s= 2 ( 1 ) gt 2 ( 位移单位: m , 时间单位: s , g=9.8 m/s 2 ). (1) 计算 t 从 3 s 到 3.1 s,3.01 s,3.001 s 各段时间内平均速度; (2) 求 t = 3 s 时的瞬时速度. 2、已知点 A ( x 1 , y 1 ) , B ( x 2 , y 2 ) 为函数 y = x 3 曲线上两不同点.

相关题目: 点作直线运动，已知某瞬时加速度a=-2m/s2，t=1s时速度为铆，=2m/s，则t=2s时，该点的速度大小为(); 某瞬时若平面图形上各点的加速度方向都指向同一点，则可知此瞬时平面图形的角速度ω和角加速度a为（　　）。[2012年真题]; 直角刚杆AO＝2m，BO＝3m，如图4-2-15所示。已知某瞬时A点的速度v_A＝6m/s，而B点的加速度与BO成θ＝60°角。则该瞬时刚杆的角加速度α为（　　）rad/s2。
图4-2-15; 动点作匀速直线运动,则下列说法正确的是( )。; 动点某瞬时的绝对速度等于该瞬时的牵连速度与相对速度的矢量和。( ); 14一质点作直线运动,某时刻的瞬时速度为v=2m/s,瞬时加速度为a=－2m/s2，则一秒钟后质点的速度（）。得分：2分; 一物体做变速直线运动,已知路程与时间的函数关系式为S=t3+10则物体在时刻t=3时的瞬时速度为(); 质点以速度v=4+t^2作直线运动，沿质点运动直线作Ox轴，并已知t=3s时，质点位于x=9m处，则该质点的运动学方程为（）。; 有一质点沿x方向作直线运动，质点的运动学方程x=4t+1/3t^2-12决定，其中x的单位是米,t的单位是秒。则质点的加速度为（）。; 一物体以初速度υ₀、加速度a做匀加速直线运动，若物体从￡时刻起，加速度a逐渐减小至零，则物体从t时刻开始（）; 地震勘探的理论基础是（），它包括运动学和动力学2方面的理论知识。; （2012）动点以常加速度2m/s2作直线运动。当速度由5m/s增加到8m/s时，则点运动的路程为：（）; 点作直线运动，已知某瞬时加速度为a=-2m／s^s，t=1s时速度为v₁=2m／s，则t=2s时，该点的速度大小为（）; 绘图题：已知直线MN外一点P，如图E-4（a）所示，过P点作直线MN的垂线。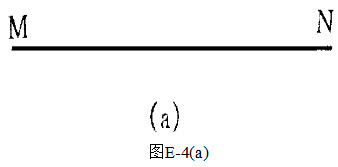; 如图4-42所示，直角刚杆中AO=1m，BO=2m，已知某瞬时A点的速度νA=3m/s，而B点的加速度与BO成θ=60°，则该瞬时刚杆的角加速度为（）rad/s2。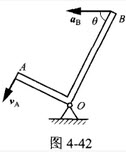; 点作曲线运动（如图所示），若点在不同位置时的加速度a₁=a₂=a₃是一个恒矢量，则该点作下列中的何种运动（）？; 已知A=40；B=30；C=100；D=50，逻辑“与”运算符为and，“或”运算符为or，“非”运算符为not。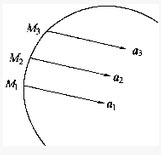计算表达式（A>B+20）or（B+60<>; 平面运动刚体在某瞬时为瞬时平动时，其角速度ω和角加速度a是：（）; 图示瞬时，作平面运动图形上A、B两点的加速度相等，即a_A=a_b，则该瞬时平面图形的角速度ω与角加速度a分别是：（）; 点在某瞬时的速度为零，那么该瞬时点的加速度也为零。

广告位招租WX:84302438

题库考试答案搜索网

免费的网站请分享给朋友吧