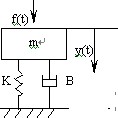
A、<img class=\""kfformula\"" src=\""data:image\/png;base64,iVBORw0KGgoAAAANSUhEUgAAAPoAAAAuCAYAAAABQwQEAAAJ3ElEQVR4Xu2cB6wtVRWGP1RENCgoxBZjATugRiUqlhgbwRasiAgSjb0bjUKwG1vUYMPesFdULBgFBAVNwN5bIoIltqgUu+Yza8ed8Zx3ZubMmZs7s3bycpP7ZmbvVf7V992JXMmB5MDkObDT5ClMApMDyQES6KkEyYEZcCCBPgMhJ4nJgQR66kByYAYcSKDPQMhJYnIggZ46kByYAQcS6DMQcpKYHEigpw4kB2bAgQT6DIScJCYHEuipA8mBGXAggT4DISeJyYEpAV1a7gAcAPwIuDfwduC0bS5m6bozcH1gZ+BmwPODxm1OWh5\/LA5MCeg3Be4IvBr4B3Ag8FrgQcD3xmLoBva5OXBr4HjgX8CDgYcDRwDnbmC\/\/OQEOTAloAuAh8a\/88MDvh94EeDP7biUz5OBk4HvBAHXBN4DvGob07UdZbGtzzwloF8K2BW4APg3oCd8RwD\/7BGkZHh9NHAT4K\/APYFz1tz3MsDLgcsBjwvargS8G\/hCGLE1t5jV66Y9Gv4bABpM07uPz4EDUwJ6LS9B\/xzgj8ArI5QfQ56XBY4DrgUcBvxmgE01XpcMkPu5awPvAl4KfGyA78\/tE+r8s4H7AA8Avj8CA5Th4WGw3e82EaF9eCzdnBrQBdr1gFsBV4x8\/c8jCLJsUcLqrwDPAP428N7Ky\/zcouPjgT8M\/P05fO4KwJuDUHmpM9jkMhp7CXAm8N6INnVET41NjdisKW10TQ3oNbNuEWHao4Efb5SL\/\/u4BcBPR5j9zg3seUPgmVl1X4uzhu0fAD4CPDeAt9YHV7xseqA3f0TDMBuZvQV4OrDx1HLKQN8tqu5W3M3L2i6jAQt7TwP+0valeO6RERYOkZ83t74y8BTgdcDPOp7Lxx8IXKcjL3psM9gr1ideFvWILw\/2VbhXpDxj5Oe7RIp1IXAs8M+KjqKfPwReuGmDMxWgXzq83NUBPbjhunmR+bnMNUxqC1q98kOi2n1xBwUr++09YH5ethfkTwDeGCBXSfYCftrhfBovgW4Pfjusws8TgC8NdOCSn1s\/uR\/wzYG+u+wzVwtDZcFPXayXOvtiYE\/gsaGzGzvOVgDdQpW50XmAuYqtsN8DKrPh1LJ8RcU2BPo78Gtg\/wjBvgX\/\/ZNYMsu+8ifCOgp6B2YMj97XgYN9gV6E+oMY0lGAVt9vBLwC+PmSM+yILl8xx9N4fbDy5J7R\/fxd27Uu0PVOzikcBOhhNWhfBT6zwBtdIuoIPv+1qHDr1SwitjWe6wJdnVBHjozCl\/UT8+SHBcPGyM8dcrK1WyKTpqz08spS2fyurSD7PDc20G8fIYyFKltPpU9sQULLvcyyaQQsaPivDL\/YZjK89ncWpVQMPbE\/BdvdwmL73S7Fjr5AN+T\/LPDdoKO01gzn7wT4s1k8W0XXnyJct8JeLyOWuwbg2sp9HaBrjJSR+5pTClqNtO1EvdXXq0MoU4eUNOieW977Oz2o0ZXGvM1aB+juZ6py\/4iEdCble8rBVK4ZSrc5U9dn1KUvhoOyJboI6KYQh266jjQm0C0kvQ14TYQz9rpdhRkyflmuohXWgxTh2G56YrRH9PJDFtv6Al0F0nKr0AK+rFKgWwTMMenqC\/TLR9ipYZVGo6kCJCcPTSlqJb5q1BFsYZXQeJ+Irj7ZoUawDtDtSni2xwCnV7JwmtDZimX5uSnRC6LP3hXUpobHAN9uyH4V0O8bRknntLE1FtDr\/FVm\/7KiaFVxpAyNOP6pNzH0K\/Pf\/p9V7i4eexUz+wC9nNEwXUD9otrEKMbhFg1SDYix6eoDdA2qBUAN7CHA54Mu80uBLKCcRqwNrZGNqZJ5sKGyy4jAvvWndpDCNOXSF+gaGjsepoYOGRl9uMbOz2sn1pR9oVW+TgroXjQ5Max6HTKpSBaH7rGD4YU6vLc\/\/TngLOAMwNB26NUH6CU\/Nx9t9s\/1gq+P8KwexR2brj5ALzmmRT+jjzZ9e9tG9ouvC+jBzedPjXRKY9129QW6BsVBFHNw6zNljd0\/nyXQnde2INUMmdoy34KUkYB5l17EJeiP6nlhRTA\/a4nGGarqFbwBt0gxLUBpnC6q3nfc1iKgfdk3VL8v7RVzxUUtt6HpMteTJ4uWXtWBomWtOSMjLwTVLSDB7XCJXr1ZNV4G2FIEc6DHsWCLYC4NYHM4RPqVgxeSmsuCnsbC6G+RQVc2yqFEDb5fKtnyocnvYrSMKsbIzz3PrIpxJUS9y4KWhlXRD8UljbbDC1p6wx1zKUHVpUfexpv08egaoDctKJCVSTnz2lUecdN0dfXoBTQaaY1rneu24aPPCHo9vLJyYrFL0amPR98jiroakGYKtSpFbEtTl+dKpHfKgrZmoU\/jO4n22o76yzXz9Yh6AS1uyfn0hHqBR8XvC5PLTLkV7raepq2A+gC9DNgI+LqoYhhpi89uQD2XvhV0dQV6kZs5d5OuZRGDEYFjv+bGtRe2TqFBNm9vO+zTB+jlwo+tTIu1JerS4FgoMyq0WPqTOKNXf+tzDl2MKzR4jmZKV6LZb0xlYKYw+baNfqFWV5CqSF4uMESz2GZLxvnjwqR9wxvWADK0tqrqxZWhhx76AN13vMwimMo59S5GHF5sKS0pAbJVdHUFumfVm9uHXgR0Q2s9tLMLVpZLd8FwunmRyGjGYR0LeG0Lp32AXt4pZy89+6tECmJLUD4442BUaGu2TlXaOoMuz5muWv23aFkXoY1m3xpObDIjsM6d21ZT4N6rNnfV6hvOKwQVSQt3y2jN2HrTQPiMwKnbVb77pKjelksCXRi\/6tk+QC+gtn1orlsuLdw4pvLqW2xbRVcfoNsLd8jFYqIdg9IS1UhbC7COoWz8vc8qr+c1vKSGWnnpUU1h2q4+QPfbTWDppb0f4B\/vMFLU06tvGqjSRWh7pj7PySudlwXkwkP1Qw\/v8NekLrWo3E5JGapbzDJvswXjRJxe+VeAHsI57hoUgvrgKOg4E2xByXc\/Gp68KF4fASx7pw\/Q\/ZYeS0U3whDgVptPium45l5bQVcfoHvua8Rknu0qgWKBzFDUQZnmNJdg11P+NuTo7IR\/H0BjUdpcbWXVF+iCyPB8vzivOqMB3j2KcE5S6umtqTi5OMYqhtGUU\/24XfTbHR4a5Qxj9dHHYOZQe\/QF+lD7b+o7fYG+qfOs+m5foK\/67iz\/P4H+\/2I3d7p7hFRD3yffSiVzJFjvXO5ib+VZ2uxt1d\/LSPbih67DtNl\/Us8k0CclziQmObCYAwn01IzkwAw4kECfgZCTxORAAj11IDkwAw4k0Gcg5CQxOZBATx1IDsyAAwn0GQg5SUwOJNBTB5IDM+BAAn0GQk4SkwMJ9NSB5MAMOJBAn4GQk8TkQAI9dSA5MAMO\/Ae9TFFNkT7DzQAAAABJRU5ErkJggg==\"" data-latex=\""a{s}^{3}+b{s}^{2}+cs+d=0\"">
B、<img class=\""kfformula\"" src=\""data:image\/png;base64,iVBORw0KGgoAAAANSUhEUgAAASUAAAAuCAYAAABu1w8AAAAK2klEQVR4Xu2cBawtSRGGv8Ul2ALBgntwQnB3CO7urotbcFnc3RbYxR2CBAmuCe7O4gR3l3xJdTIczru3T5+eOXPPrUnIW96bme76u\/uvqr9qzkHklQgkAonAjBA4aEZzyakkAolAIkCSUm6CRCARmBUCSUqzWo6cTCKQCCQp5R5IBBKBWSGQpDSr5cjJJAKJQJJS7oFEIBGYFQJJSrNajpxMIpAIJCnlHkgEEoFZIZCkNKvlyMkkAolAklLugUQgEZgVAklKs1qOnEwikAjsFVI6PfA74NdbtGTnBq4OfD7+fD\/wJuBfe9zGg4HbAj8Ergx8AngJ8M89bldOfyIE9gIpnQp4GfBQ4JMT4TL2MKcBbgM8CfgTcFbglcB9gQ+OPfiI7z8mcB\/gdcC3gZMDLwbeDTx7xHHz1VuEwNxJ6WjAvYFDgOtsESldLKKH6wFfBk4cpPQh4NA9vL8k12sCTxlEfPcCLgfcHPjNHrYtpz4RAnMnJQ\/v+YCrAY\/YIlI6CnA84A\/Av4HTBikZOb11grU\/J\/B4wD8dWyJ5W4dxLxwp6K2A98T7bgpITDeK6KnDMPviFe57HdTZOq\/R7MGbMymdCLg98HrgucAjt4iUhhvDNbgdcA7gIZHOTbFxHPfhEYHeAPh6h0EL2ZqSqiE5hoQkWd0xI6WVER5jjXabhGNeErgs8ClAPfeEwPOm0nTnSkrO62bAV4HvA0dsISkdHTgLoOB9HuCZwE922zEd\/\/0Eoff4SknRQkLvSz3wpaEnvb33y\/fB+6ZYo0UHeWPgosADBg7yUsCdgXsCPx8b97mS0tmDrRVJZeltJKXh2p4OeA7wOOBjYy96vF\/957XAW4Lw\/9N5XPXA+wG\/BV6U1bcmdE3dLBpYlTVT6L1Gi5NyH3rmHgx8evCPFjCeCHw3nOeo85gjKR0buEsQkaysCNxKSqaATwcePXM946gxRz2j1au\/Vm7hdey7Qug+vfSkRY97Q8DNbFVx29sBjhWVVG3tWSG+RmiMY6zRsi1mMenugDrgYtRu+n2tKFj8snJ\/Nt02R1JSADad0dN6+f8fCLwC+ALwOeBvldZKaJaiFcm\/UfnMFLfdDbhuLPCPYkBbHi60YpWq1T7XXf1KLamXnlRw891WFT2orw5COnNscrWmbbx0pE8DDu8Y6RY96SaB5xdHBq44RtdqWTovQT55irlsipROGprRPyJHVVcxTP3SEuDXiZRaD22Zhp7eyt8FghDPBLw5hNsPRDi7bK8o+JqHXyZI1AqXB9KI7y9R7TpZ6C1GEccHnhXtAU9doYGy1T6J3nTRPyV77foxYLXTVMuGzha7fOYSgH1Ypoba5oG1rcNixVQtAa6b2Nu8aeRyRuCz0S+1mHrstlY1XLAuKXkOPQO3BL4S1baPRxOq44+l+Q1tKzb4dxYn3KfDy73xUeDiHYl3KbabICUP4xPif1+LWXm41B\/8++HG9TBfOvJpD+174+BaRq+5Wg+t7z4u8NiYj\/m0i2QlQu9vRHPFmM\/iPMRUsdD83OdKFcrowW5t9QGjwGvH+\/SAF4n2ACscq0QTrfZJQq8BThICps2NHlZTOityFhksMAyvGrv0skYL4jO8JKRV0tKatT3QPTo8+6Rst7h\/4Cne6iS2PQwJt8ammrmsQ0rOwVT3+sA9wjmU95ky2RZgFD12p3\/plXPddyIlWzt0OKNdmyAlP0HQcxWgDRtV9U0jPAx2Ave6Wg+tm9hDpNfXS\/0sJlQ2iyVuN9KylPAUERV4uEvILQnYlf6Ozs2RrfYVPekOIWyW6KGI3x6ExY03pV2t62\/EaRolLh5oNcly6I0MPfTqPuXqZdM6pGRE7dzUUT88mNstgJfv0ENm9VZH7vMtlz1x7xs8WEtKntEhhi1j7\/jM1KSkzqAXM9LRixl9OIfLhwbxrs6iaOuhtU\/DSELi9LutctWUaCUsn1ULMAT30nsrIr4zvgnrtZCt9j0IuPUSfaBUe+wNszgwvKa0qwUfnZtpomtmFOq3hF7HiOjPw2tT59Dp9bKplZQkRdNndUV1xhIlT60nidO+JaXSTCcx2ZglU\/vB5keA37fsxF2eaTm0pfx5lSWH1rz\/DcCrdijRlhTPVMbISE1D\/cmoqjbtrIWixb6iJ3mQFrWKEkGZ6ix+7tLbLiuHh0UkUGtvuU\/dy0+P\/jx4sER5lq2Nxmv0q142tZKSjuqNsQ6rOr9VMdvt\/n1LSgKjVmNoavpTQk8JSs9dNKbdABz+u1GI2s0plzxkiKv31zsuCnfeLhF6AL81eFYdS9KxJLp4aGtKtEW0tLRqBOj7vKwgSsarlsfHss\/v7IZaxdBhLCtB97ZrlTWuuVcissfGaMkUruZaxSb37cOA8y55sWK5TuinB3CuOiMjzxI5lwjOT33UaPy1iM8sIVgj6yn0JIfe10L3cE0FwtL4Y4AXdNZbSki6akuAIb3fbfnccEOUkqnVuNoyupteb6x9dm\/3\/v6rJVIq9vkJz1A3KqnpqUOo\/94Op3psu2oIZXiPKZoHXIFWRzfUZmrftY5NLZGSkaJFAclusS+oxvnV2lV7X9nf54\/5\/GrhQeeoTmrBZtT2hCk1JasLRgp3Cm2l2Hwc4BnxSUmth6sFuuXQltKn5Vnz\/XIt6kn+LIcVOKuCXkY0\/vffQx8YpqNqVKZD6kxH1k6+4r517Fss7V4wurutgPrJSxG\/N2FXhen\/c0tNAWL4QG+bWkippEv+7pSFnpKKlh4yswkJ4Duxn6zMDvdUb6FbfCQeBfdl+1TCd7\/7aw9b0TxZFs2v0g2zh1UrxT6rDzY49mbglkNbtAmrE8Mqgx8o2mf0wtCTDLm9ytf1kplCvWG65DpM07T5DOFpVk3fdjqg69h310G\/iTqa7Q9WCUvVqoy7CbtWJSXv99DoSJZVRU2vjFJ\/EL02vW1qIaUDpUvlN6isAEsStm2YTegsxm4LsI3FKrF7uBQKxLbokKaYQ4fVsk67PjNVpOQ4Vhcko\/KTFk7Ow6Bgqbew\/6f3NzUth7YcUD2X3xu5ESRTO6DtNHeealhWDw2\/Sz+PC6qNj1rwaD6rjT7f+2PGdezTAz8\/doh9VXpAS+ZDfc1\/3oRdu27cJTc4T52GNulMyl4yPVKv1C73nn\/f26YWUtIEtTsjE6uC6lEefiuj9q2pgxpBSbKS6ZAkWvCpeab0bRnZ2xJTqoE6ZDMcddLee\/j\/5jUVKRUCumoIv9+MdEe9xQ5pI6TehOSYLYfW5\/xJVyMJG\/C8DFdtejR89fsfydXOW798H87bza5X8\/5fAH5Y\/Mc4LKs0RdZsoHXsM31xgynmWyCwm9sDfaA5Tm1Xrf2L96mH+TW7JXYPteKzzsVodlEj6WlTKykZDZminSvm67pYkfQjdPVMv3CwQGO1sfbTqlbsynNGlZLQleJXUD2j6l+SvXt69GtKUhrdmCUDtJLSJubaMua229eCySaeaSWlTcx19mNuOynZ4evvwsjypojbdm27fXtlvaz+me7Yl9ZbF90rGHSb57aTUjeg8kWJQCIwDQJJStPgnKMkAolAJQJJSpVA5W2JQCIwDQJJStPgnKMkAolAJQJJSpVA5W2JQCIwDQJJStPgnKMkAolAJQJJSpVA5W2JQCIwDQJJStPgnKMkAolAJQJJSpVA5W2JQCIwDQJJStPgnKMkAolAJQJJSpVA5W2JQCIwDQJJStPgnKMkAolAJQL\/BTS9rU3lRfoSAAAAAElFTkSuQmCC\"" data-latex=\""{s}^{4}+a{s}^{3}+b{s}^{2}-cs+d=0\"">
C、<img class=\""kfformula\"" src=\""data:image\/png;base64,iVBORw0KGgoAAAANSUhEUgAAATEAAAAuCAYAAABAki6SAAALZUlEQVR4Xu2cBcw0SRGGn8MlcBAguBxO8OAeEiwEd3d398PhOPwOd3eH4O4Q3N3d7XDNE7qTztzufjO9PbPf7FYnly+3\/+5MV1X322+9VTMHECM8EB4ID8zYAwfMeO4x9fBAeCA8QIBYLILwQHhg1h4IEJt1+GLy4YHwQIBYrIHwQHhg1h4IEJt1+GLy4YHwQIBYrIHwQHhg1h4IEJt1+GLy4YHwQIBYrIHwQHhg1h4IEJt1+GLy4YHwQIBYrIHwQHhg1h4IEJt1+GLy4YHwwDaD2IHASYBvb0GYzwVcGfh8+vte4PXAv2dum+vvMsBZgKMD5wUeAXxr5nbF9Cf0wLaC2NGAhwFHAIdM6M8xbnUa4BbA44A\/pw3\/MuBewAfGuOGE1zwfcBHgGcB\/gBsCtwJuAvxwwnnErWbsgW0FsUsBTwPc7HMHsYsBzwOuBXwZOFGy64Mzt821d3fgncBX0h46LfBy4HDgVTPeVzH1CT2wjSBmCnlT4OTAryfc6OcAHgP41814VeDNDWJ5FOB4wJ8SW\/HagrPM7E0Nrr+pSxwLeAJwXOBOiTXvF4A+XVo3premuvcAnrQpR8V9V3tg20BMe0y9PpVA5F8Tgpie9v4PAa4BXAf4euMF6PVNt84OPDCll41vMenljg0cNQGYNz4IeCnw2H0C0Ka1LwJk9h+a1DPzuZkxvFE6jFzvF03M+nWA+2\/0sW0gpgB+AeD5wIOSE6dMJy0mPDdFTbD5Q6MIKnqfGdC+c6d066eNrr1fLpMBWsC4M\/C7DU\/sGIlZXwi4AfCDDc9nP95eFn0o8DHgFcB\/AfXoe6bJyrRHB7JtAjEdevt0cv4KOHgDIGbqoZbzxlRYMKith6mOet+jgY+2vvgGr3c24P77qDqpLKE+933grsBfNuib\/XprJRNZ2G06h46MWh33PsCnx578NoHYNQHBK9P+WhA7IfDktJmGtmdcFnhXQz1sUfxNv2xDkPV54v2t5yJZx66et6j+2kmT7vT0SsZzXeD0jaUDK6dvSdrjWHqYuqDaphrnJ6q9t5kfHjOl\/VbM3Wtlu48argftN4FHJYY22iy3BcTc2OcETlB4yhRAKvvqVNVT5O8zFJefCjwU+EafH6Tv6Et1KrWwlnqYorcAfWPgx+leLhrTHD\/rm3bV2jXABVVfFcDuAjw7AZgbQBb03QFXszVDEBPcW42sh10OeHeri3auo54kQL5khqz6FAl8LV51QT6n4icG7piKUiO58P9C9NTDdEi9yA1p\/vwT4LeAi9kGzmU5tAtb6vpP4BdJHxKgvrTEgFomVrvZ8+nj3xcDZ0y22SLxnNSoumiqVh\/VgS4NfC5VNj3dFLj\/mlidvlHn0zfHB56SgPmJAxpea+0q52zPmoDhqftzwP9\/VmLAi2zbK2ZZAnhNwcD0lxvEz\/qOdUHMNXnrtK5kR99LAvUFV+hhe8Wtz9xbgJg+1n6HMTl\/isnYDcNZOslMsmuv+89YOrff9HFG7XemBrFLJup5P+AzqZpnr5ACoKfRMtR2Eysg+t\/XkrFuynunz0o2IojIUu6WwFEA+eyASl7tZhe0Xgl4+qjNvSPRaFNMK5YCsPpKOfT\/9QE3kRU5QcrP7AkTKAR1gf7qqXL3xdQcaruFDaKCXd9Ra5fXd07O4cFJH7JHzWGhwc8tnvyjM5G9YvbHlEJqdzm0TfYzJL1aB8TymnQd2ocnq1fLUXNctib7xK1PXNYBMedwNeAOQN5P3lM9SvZurIasjz7zLb8jQH0krWvT4UUgpmZ2vbGfmpkSxBRuX5BSNY3Oond2hsi9LH++JXCGIvd2oSm2mrYJDkO1q1UBq93sWQ9T5LRCme3LJ5YbvdvAaS+bOpAgJ0A5BMMXAm9trPHU2uWcrpAqoqbYuQolSMkIZYaLTtspY1YLYnlNake5EQU2gXpZf1iruNWCmPtWHVAm7oFZ9gvKzHxaRWmje7g\/EjjrULRKuqvXE+Tz6ANiyiDOc4gsM3h6U4FYDpZApNbws2KmV0lBWNYcmpsifSzFE9IUKz9z57+9vXEZt3azW1m7eWJRGZA000Vj2mt61NVsLpzYm\/qdZWqHi9A+s7cBPxoc0eU\/qLXrTImRyIA94fPpfp6U8prmHtZJa6eOWQ2ImcqqfZ5qwZrcSw9rFbdaEJO5Kzf8EvCwKMFKFmuT7uMHSA01y2znQExtwbYDGUZZyciVtiutEMPz4ymmnJ8E3gN8HPgwYErSetRs9qyHuSi7\/WGZoT1gAbOS+stsBAqZlynU+9PJJWi3HDV2lamVp6rpbZ8xdcxqQCyvSVmzzCVX1\/r0h7WKWy2I3RZ4ZsEUlRxOlgpAPtEh41JnHnPsHIipN0h9u2yrb3Oop6ano9RUEdwhoMl8skY2JGCyHbUYBeTusLFU9mSKKuvrDoFTQCqF0\/zMnylICdLlZl7ENP13dSWbO32bg9dxqHHUNAq2tsu0ySLFcSoaPlvHTG3FeC8a2u0clzWkytZNGcs2gGVrUk1TLcx2nWUa7ZC46Qf1KZlrd1gc8AAzM1l0IHuQyd4zS\/f3Gfhk72rCOVXTdufsSw+mGDsl7OfUQkaiYF2mWm7g16amQk\/DPs2hBlFW4GljZax1R34NYzG9sD\/MClepe2WQPnUS8K16LRtuDE947bI7v7UgWmNX7pWSJa7T8Dl2zIYysVVrcmh\/2Dpxq2Fi+flS2f8mnyTILRbvWyCTZLs8WLaixaLUw3S6p0UepR5mY6GMRC0oC\/XXTozkdunz\/Dudow7z1REezK3Z7JlaX7zT75NTFquqvpkhg7TMQWZgRU+dqTyFFZUF5tYLdB27ZBJ9e7A2EbOhILZqTXot9Sa1JTeoPWwetOqTreNWA2L5YBTEhrQv+P2Wwn6eu08ymDmU1ek8xy9sS7NrbgJ1g5dOl2bbJCeLscoopVa4N83zmcPsJN8KoXhZVjhMc+wItlpWMrsWNLpms2dq7amTHwWyo9lqq9VGNQx72\/IQ9ExxBAZ9UPbGaauNm1YsWz53VmNXTpNtF1kEYqdMMTUWCv6bitlQENtrTXr4KF3Y32Ta6dtJbP1oHbcaEFOndG34HrYuKXB9ua8EFfXn77TYECuuoURii8fNOsU6MywLPpKPrXnsyAY8K0FuUN8d5QaXgZhiKki6YERvH9625UDG4kLzO4KXqVoe\/tYeME\/GXO5vGauazZ4By0Wj4Oqw\/8uOek\/ybuOh1SVte3iHhQnY2mY5uwS9FvbV2GUMnL9xsmBhM6XDz62AXTHFK4vIm4rZUBDThkVr0g0pA1MoFyDcjDb02hrkaB23GhBzHraG2CcoQy7friFTNJuxiGZv5NhDwJR0WGjLbVP6ThC1Kb1G1x0856laLLyPHemmjzpX7cfGUBe\/bMrNocgpgJXppuDgRpER+ByWQfK3b0gMrI+GNtQpNZvde+QF5Nsl1At8EsG0ZFnDoRtCbc\/HobTZhakou+o3Q20pv19rl4vSuPmKFdMr0xIZmAvX4kq3irqJmNWA2KI16Wt3jFdek6ZI6q6\/LxzZMm61IOZ0fMzO107ZNC5LtEDg68vNBBYVpNZZO6t+K5BZcFHiMSu6ROons5L997FuWl53KhCbwpZW96jd7K3uP9Z1ttUu\/VUDYmP5ech11wGxIffZ6u8GiB05vHag3zelhS2bTTe9kLbVLv16ecAKcH6X26Z93ff+9qT5JhKrv6213b5zmP33AsRmH8IwIDyw2x4IENvt+If14YHZeyBAbPYhDAPCA7vtgQCx3Y5\/WB8emL0HAsRmH8IwIDyw2x4IENvt+If14YHZeyBAbPYhDAPCA7vtgQCx3Y5\/WB8emL0HAsRmH8IwIDyw2x4IENvt+If14YHZeyBAbPYhDAPCA7vtgQCx3Y5\/WB8emL0H\/gejheNNbRPRLQAAAABJRU5ErkJggg==\"" data-latex=\""a{s}^{4}+b{s}^{3}+c{s}^{2}+ds+e=0\"">
D、其中a、b、c、d、e 均为不等于零的正数
查看答案
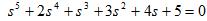 试用劳斯判据判断系统的稳定性。
试用劳斯判据判断系统的稳定性。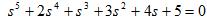 试用劳斯判据判断系统的稳定性。
试用劳斯判据判断系统的稳定性。
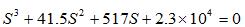 试用劳斯判据判别系统的稳定性,若不稳定请说明有几个根具有正实部。
试用劳斯判据判别系统的稳定性,若不稳定请说明有几个根具有正实部。