计算题：某生产商通过统计分析得：需求函数Q=1000－4P成本函数C=6000＋50Q如果公司以利润最大化为定价目标，则其价格为多少时可取得最大利润？最大利润是多少？ -题库考试答案搜索网

计算题：某生产商通过统计分析得：需求函数Q=1000－4P成本函数C=6000＋50Q如果公司以利润最大化为定价目标，则其价格为多少时可取得最大利润？最大利润是多少？

问答题

2022-01-02 12:05

查看答案

正确答案

设利润为Z，销售收入为R。依据成本、收入和利润之间的关系，可建立下式：
Z=R－C
=PQ－C
=P(1000－4P)－(6000＋50Q)
=－56000＋1200P－4P<sup>2</sup>因此，利润是价格的二次函数。
根据二次函数求极值的原理，欲使Z最大，则：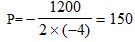
最大利润Z<sub>max</sub>=－56000＋1200×150－4×1502=34000

试题解析

标签：市场营销学经济学

感兴趣题目

价格某产品生产的总成本函数是STC＝Q³－4Q²＋4Q＋70。写出固定成本函数。

已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数LTC=Q3-12Q2+40Q。试求：（1）当市场商品价格是P=100，厂商实现MR=LMC时的产量，平均成本和利润；（2）该行业长期均衡时的价格和单个厂商的产量；（3）市场的需求函数为Q=660-15P时，行业长期均衡时的厂商数量。

某寡头垄断市场上有两个厂商，总成本均为自身产量的20倍，市场需求函数为Q=200-P。若两个厂商同时决定产量，产量分别是多少？

假定某厂商的边际成本函数MC＝3Q 2－30Q＋100，且生产10单位产量时的总成本为1000。求：（1）固定成本的值。（2）总成本函数、总可变成本函数，以及平均成本函数、平均可变成本函数。

价格某产品生产的总成本函数是STC＝Q3－4Q2＋4Q＋70。写出固定成本函数。

价格某产品生产的总成本函数是STC＝Q³－4Q²＋4Q＋70。写出平均可变成本的函数。

已知一垄断企业成本函数为：TC=5Q²+20Q+10，产品的需求函数为：Q=140-P，试求利润最大化的产量（）。

已知某厂商产品生产的总成本函数为TC=Q3-4Q2+100Q+70，求：总可变成本函数TVC、平均成本函数AC、平均可变成本函数AVC、边际成本函数MC。

垄断厂商的需求曲线为Q=D（P）=100-2P；成本函数为C（Q）=2Q；则它的最优产量水平是（）

计算题：
已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数LTC=Q3－12Q2＋40Q。试求：
（1）当市场商品价格为P=100时，厂商实现MR=LMC时的产量，平均成本和利润；
（2）该行业长期均衡时的价格和单个厂商的产量；
（3）当市场的需求函数为Q=660－15P时，行业长期均衡时的厂商数量。

已知某产品的生产成本函数和销售收入函数分别为：TC=180000+100Q+0.01Q2，TR=300Q-0.01Q2，试求其盈亏平衡产销量和最大盈利产销量。

某商品的需求曲线是Q=50000-200P，供给曲线是Q=-15000+300P，现假定对每件商品生产会产生30元的外部成本计算该商品在考虑社会成本时的最佳产量和相应的市场价格