由曲线与直线x=1及x轴所围图形绕y轴旋转而成的旋转体的体积是().
由曲线y=ex,y=e-2x及直线x=-1所围成图形的面积是:()
曲线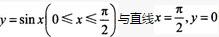 围成的平面图形绕x轴旋转产生的旋转体体积是()。
围成的平面图形绕x轴旋转产生的旋转体体积是()。

设D为曲线 与直线
与直线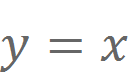 所围成的有界平面图形,求D绕x轴旋转一周所得旋转体的体积V.
所围成的有界平面图形,求D绕x轴旋转一周所得旋转体的体积V.
 围成的几何图形S的面积,以及图形S绕x轴旋转所得旋转体的体积。
围成的几何图形S的面积,以及图形S绕x轴旋转所得旋转体的体积。
设D为曲线 与直线
与直线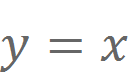 所围成的有界平面图形,求D绕x轴旋转一周所得旋转体的体积V.
所围成的有界平面图形,求D绕x轴旋转一周所得旋转体的体积V.
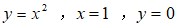 所围成的图形绕y轴旋转所得旋转体体积V=________。
所围成的图形绕y轴旋转所得旋转体体积V=________。
由曲线y=x2/2和直线x=1,x=2,y=-1围成的图形,绕直线y=-1旋转所得旋转体体积为:()
免费的网站请分享给朋友吧