直方图均衡化是通过灰度变换将一幅图象转换为另一幅具有均衡直方图，即在每个灰度级上都具有相同的象素点数的过程。
直方图均衡化变换：设灰度变换s=f（r）为斜率有限的非减连续可微函数，它将输入图象Ii（x，y）转换为输出图象Io（x，y），输入图象的直方图为Hi（r），输出图象的直方图为Ho（s），则根据直方图的含义，经过灰度变换后对应的小面积元相等：Ho（s）ds=Hi（r）dr
直方图修正的例子：
假设有一幅图像，共有64（64个象素，8个灰度级，进行直方图均衡化处理。根据公式可得：s2=0.19+0.25+0.2l=0.65，s3=0.19+0.25+0.2l+0.16=0.8l，s4=0.89，s5=0.95，s6=0.98，s7=1.00
由于这里只取8个等间距的灰度级，变换后的s值也只能选择最靠近的一个灰度级的值。因此，根据上述计算值可近似地选取：
S0≈1／7，s1≈3／7，s2≈5／7，s3≈6／7，s4≈6／7，s5≈1，s6≈l，s7≈1。
可见，新图像将只有5个不同的灰度等级，于是我们可以重新定义其符号：
S0’=l／7，s1’=3／7，s2’=5／7，s3’=6／7，s4’=l。
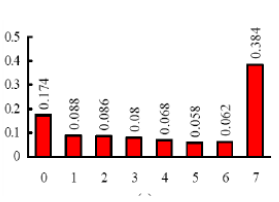
因为由rO=0经变换映射到sO=1／7，所以有n0=790个象素取sO这个灰度值；由rl=3／7映射到sl=3／7，所以有1023个象素取s1这一灰度值；依次类推，有850个象素取s2=5／7这一灰度值；由于r3和r4均映射到s3=6／7这一灰度值，所以有656+329=985个象素都取这一灰度值；同理，有245+122+81=448个象素都取s4=1这一灰度值。上述值除以n=4096，便可以得到新的直方图。