X1和X2是任意两个相互独立的连续型随机变量，它们的概率密度分别为f1（x）和f2（x），分布函数分别为F1（x）和F2（x），则（　　）. -题库考试答案搜索网

X1和X2是任意两个相互独立的连续型随机变量，它们的概率密度分别为f1（x）和f2（x），分布函数分别为F1（x）和F2（x），则（　　）.

单选题

2022-01-11 16:19

A、<img src="https://static.tiw.cn//s/tiw/p3/UpLoadImage/2013-05-07/346cebff-889e-4c61-bfc9-f0af08841260.png" width="85" height="24">必为某一随机变量的概率密度
B、<img src="https://static.tiw.cn//s/tiw/p3/UpLoadImage/2013-05-07/da5a2be4-5778-4793-a4c7-85ac63ccd3c1.png" width="72" height="24">必为某一随机变量的概率密度
C、<img src="https://static.tiw.cn//s/tiw/p3/UpLoadImage/2013-05-07/20b3e5d0-d552-45c6-9aea-26bf3d02ee6a.png" width="88" height="24">必为某一随机变量的分布函数
D、<img src="https://static.tiw.cn//s/tiw/p3/UpLoadImage/2013-05-07/4fa715ea-e461-417f-82ac-a50d91cf5f76.png" width="73" height="24">可能为某一随机变量的分布函数

查看答案

正确答案

D

试题解析

采用举反例排除的方法.对于A项，

不能作为随机变量的概率密度函数.
对于B项，

不能作为随机变量的概率密度函数.
对于C项，若0F（x）=F1（x）+F2（x）则F（+∞）=2≠1，不满足分布函数的性质，故排除C.
故应选D.

标签：考研公共课数学

感兴趣题目

下列关于两个相互独立的随机变量X1和X2的标准差和方差表达式，正确的是( )。

如果两个随机变量不相关，则这两个随机变量一定相互独立。

设两个相互独立的随机变量X和Y的方差分别为4和2，则随机变量3X-2Y的方差是（　　）。

设X和Y是两个相互独立的随机变量，其概率密度函数分别为

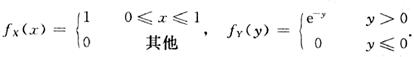求随机变量Z＝X＋Y的概率密度函数。

设随机变量X1与X2相互独立，它们的均值分别为3与4，方差分别为1与2，则y＝4X1+2X2的均值与方差分别为( )。

设随机变量X1与X2相互独立，它们的均值分别为3与4，方差分别为1与2，则Y=4X1-2X2的均值与方差分别为( )。

X1和X2是任意两个相互独立的连续型随机变量，它们的概率密度分别为f1（x）和f2（x），分布函数分别为F1（x）和F2（x），则（　　）.

两个互相独立的x2分布随机变量除以各自的自由度以后二者再相除之商所构成的随机变量的概率分布模型是

若随机变量X1，X2，X3相互独立且服从于相同的0-1分布P{X=1}=0.7，P{X=0}=0.3，则随机变量P{X=0}=0.3.则随机变量Y=X1+X2+X3服从于参数为____的____分布，且E（Y）=____.D（Y）=____.

设随机变量X的概率密度函数f（x）＝1/[π（1＋x2）]，则Y＝3X的概率密度函数为（　　）。

相关题目: 若两个随机变量X,Y相互独立,则它们的连续函数g(x)和h(y)所确定的随机变量( ).; 设X1与X2是两个相互独立的连续型随机变量，它们的概率密度分别为f1(x)与f2(x),分布函数分别为F1(x)与F2(x),则（）; 设随机变量X1X2，相互独立同分布，且E（x1）=1，D(Xi）=1，（i=1,2，,令S9=∑Xi，则对任意 ξ＞0，从切比雪夫不等式直接可得（）; 如果离散型随机变量X1X2LXn相互独立且皆服从0-1分布B（1，P），则当n充分大时，离散型随机变量X= ∑ Xi近似服从（）分布; 设随机变量X1X2Xn相互独立，Sn=X1+X2+Xn则根据列维-林德伯格中心极限定理，Sn近似服从正态分布，只要X1,X2,Xn（）; 设随机变量X1,X2,相互独立同分布，且E(X1)=1，D(X)=1,(i=1,2,,,令S= ∑ X1则对任意ε＞0，从切比雪夫不等式直接可得（）; 设随机变量X1X2Xn相互独立。Sn=X1+X2++Xn，则根据列维-林德伯格中心极限定理，Sn近似服从正太分布，只要X1X2Xn（）; 设随机变量X1，X2的概率密度分别是则E（2X1-3X222）=（）; 设两个相互独立的随机变量X与Y的方差分别是4和2，则随机变量3X-2Y的方差是; 设两个随机变量X和Y的数学期望分别为4和2,则随机变量3X-2Y的数学期望是( ).; 如果(X,Y)是连续型随机变量，下列条件中不是X与Y相互独立的充分必要条件是，其中x，y为任意实数; 设两个相互独立的随机变量X与Y的方差分别为4和2，则随机变量3X-2Y的方差是; 若随机变量Y=X1+X2,且X1,X2相互独立。XI-N(0,1)(i=1,2); 设随机变量X1,X2,,Xn相互独立，Sn=X1+X2++Xn,则根据列维-林德伯; 设x1,X2n是独立同分布的随机变量序列,且EX=∠,DX2=2(=12,)那么依概率收敛于; 随机变量是X1和X2服从的分布分别是N（）和N（），概率密度函数分别是21，σμ22，σμP1（x）和P2（x），当σ1<>; 知某个连续型随机变量X的数学期望E（X）=1，则X的概率密度函数不可能是（）．; 设随机变量X1，X2，…，Xn相互独立，Sn=X1+X2+…+Xn，则根据列维一林德伯格中心极限定理，当n充分大时，Sn近似服从正态分布，只要X1，X2，…，Xn( )。; 设随机变量是Xi服从于参数λi（i=1，2）的泊松分布，且X1、X2相互独立，则P{X1=i|X1+X2=k}=____.; 10.设F1(x)，F2(x)分别为随机变量X1和X2的分布函数，且F(x)=aF1(x)一bF2(x)也是某一随机变量的分布函数，证明a—b=1．

广告位招租WX:84302438

题库考试答案搜索网

免费的网站请分享给朋友吧