半径为0.1m的圆盘在铅直平面内转动，在圆盘平面内建立o-xy坐标系，原点在轴上，x和y轴沿水平和铅直向上的方向。边缘上一点A当t=0时恰好在x轴上，该点的角坐标满足θ=1.2t+t 2（θ：rad，t：s）。⑴t=0时，⑵自t=0开始转45º时，⑶转过90º时，A点的速度和加速度在x和y轴上的投影。
。
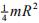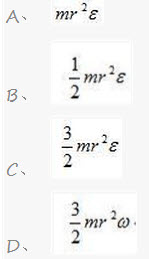
平动时，则圆盘动能T=（ ）。
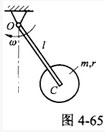
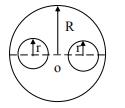
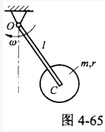
如图4-65所示，忽略质量的细杆OC=ι，其端部固结均质圆盘。杆上点C为圆盘圆心。盘质量为m。半径为r。系统以角速度ω绕轴O转动。系统的动能是（）。
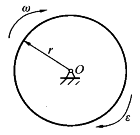
图示均质圆轮，质量为m，半径为r，在铅垂平面内绕通过圆盘中心O的水平轴转动，角速度为ε，此时将圆轮的惯性力系向O点简化，其惯性力系主矢和惯性力系主矩的大小分别为（）。
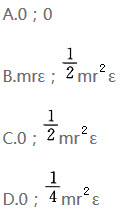
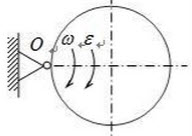
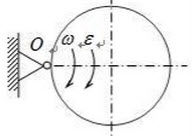
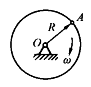
质量是m，半径是r的匀质圆盘，在铅直平面内绕通过边缘上的一点O的水平轴转动，圆盘在图示瞬间的角速度和角加速度的大小分别是ω和ε，则圆盘的惯性力对点O的主矩的大小是（）。
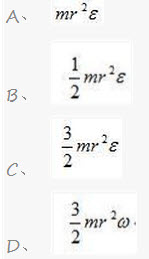
半径为R，质量为m的均质圆盘在其自身平面内作平面运动。在图示位置时，若已知图形上A、B两点的速度方向如图所示。a=45°，且知B点速度大小为vb。则圆轮的动能为（）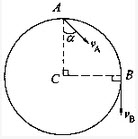
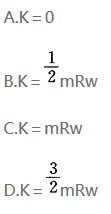
免费的网站请分享给朋友吧