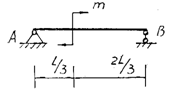
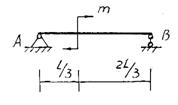
某简支梁AB受载荷如图所示,现分别用RA、RB表示支座A、B处的约束反力,则它们的关系为()。


某平面任意力系向O点简化后,得到如图所示的一个力R和一个力偶矩为MO的力偶,则该力系的最后合成结果是( )。

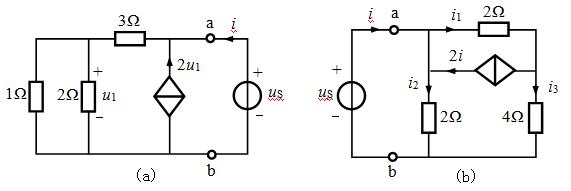
 的几何意义为:()
的几何意义为:() 

某简支梁AB受载荷如图所示,现分别用RA、RB表示支座A、B处的约束反力,则它们的关系为()。

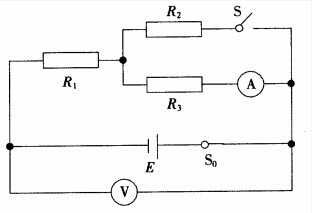
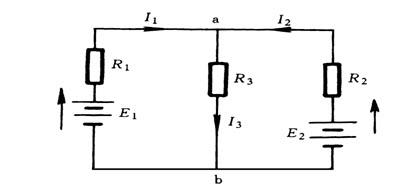
如图所示,E为内阻不能忽略的电池,R1,RR2,R3,为定值电阻,S0、S为开关,V与A分别为电压表与电流表,初始时S0与S均闭合,现将S断开,则()
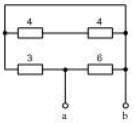
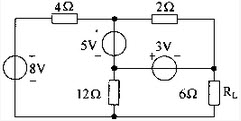
电路如图所示,用叠加定理求电阻RL消耗的功率为()
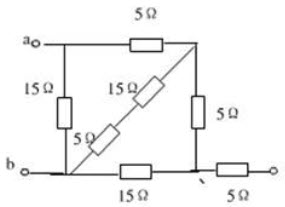
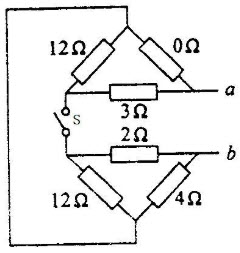
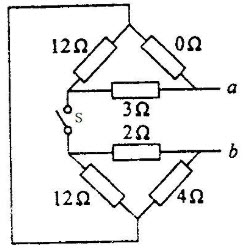
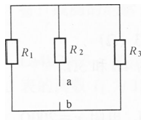
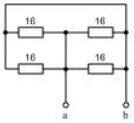
如图D-5所示,已知R1=5Ω、R2=10Ω、R3=20Ω,求电路中a、b两端的等效电阻Rab是多少?
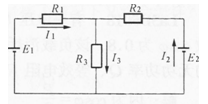
如图D-6所示,已知E1=4V,E2=2V,R1=R2=10Ω,R3=20Ω,计算电路中I1、I2、I3各等于多少?
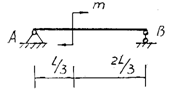
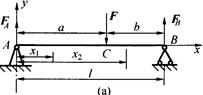
计算题:图a所示简支梁AB,在C点受集中力F作用,列出弯矩方程,并画出弯矩图。
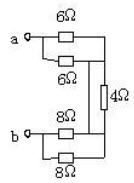
如图所示的电路,利用戴维南定理求支路电流I3。已知E1=140V,E2=90V,R1=20Ω,R2=5Ω,R3=6Ω。
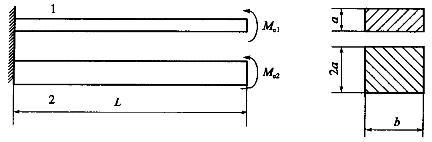
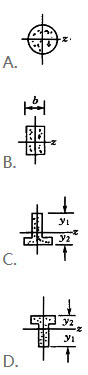
两根矩形截面悬臂梁,弹性模量均为E,横截面尺寸如图,两梁的载荷均为作用在自由端的集中力偶。已知两梁的最大挠度相同,则集中力偶Me2是Me1的:()(悬臂梁受自由端集中力偶M作用,自由端挠度为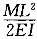 )
)
当力P直接作用在简支梁AB的中点时,梁内的φmax超过许用应力值30%。为了消除过载现象,配置了如图所示的辅助梁CD,则此辅助梁的跨度a的长度应为()

当力P直接作用在简支梁AB的中点时,梁内的σmax超过许用应力值30%。为了消除过载现象,配置了如图所示的辅助梁CD,则此辅助梁的跨度a的长度应为:()

在力矩分配法中,分配系数μab的数值等于:()
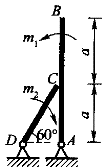
已知杆AB和杆CD的自重不计,且在C处光滑接触,若作用在杆AB上的力偶的矩为m1,则欲使系统保持平衡,作用在CD杆上的力偶矩m2,转向如图所示,其矩的大小为:()
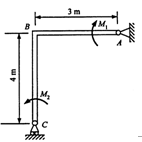
图示平面直角弯杆ABC,AB=3m,BC=4m,受两个力偶作用,其力偶矩分别为M1=300N•m、M2=600N•m,转向如图所示。若不计杆重及各接触处摩擦,则A、C支座的约束反力的大小为()。
如图所示受力分析正确的是(图中各杆重量不计)()。
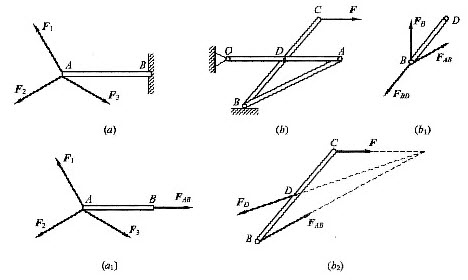
(1)图a中以AB杆为研究对象,其受力分析如图(a1)。
(2)图b中因为B点及D点皆为铰链,且B,D两点之间无外力作用,杆重不计,故AB,BD皆为二力杆,BD杆受力如图(b1)所示。
(3)图b中以BC为研究对象,由于AB为二力杆,因此由三力平衡汇交定理得D点约束力如图(b2)所示。
免费的网站请分享给朋友吧