点M沿平面曲线运动，在某瞬时，速度大小ν=6m/s，加速度大小a=8m/s2，两者之间的夹角为30°，如图4-38所示，则点M所在之处的轨迹曲率半径ρ为（）m。 -题库考试答案搜索网

点M沿平面曲线运动，在某瞬时，速度大小ν=6m/s，加速度大小a=8m/s2，两者之间的夹角为30°，如图4-38所示，则点M所在之处的轨迹曲率半径ρ为（）m。

单选题

2021-12-25 11:45

A、1.5
B、4.5
D、9

查看答案

正确答案

D

试题解析

标签：第四章理论力学电气工程公共基础

感兴趣题目

液体在某点流动时的速度叫做流速（m/s）。

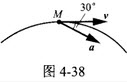
如图4-54所示，平面机构在图示位置时，杆AB水平而杆OA铅直，若B点的速度νB≠0，加速度aB=0。则此瞬时杆OA的角速度、角加速度分别为（）。

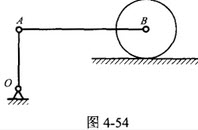
半径为R，质量为m的均质圆盘在其自身平面内作平面运动。在图示位置时，若已知图形上A、B两点的速度方向如图所示。a=45°，且知B点速度大小为v_b。则圆轮的动能为（）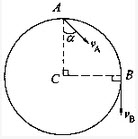

一动点作平面曲线运动，若其速率不变，则其速度矢量与加速度矢量（）.

质点沿x轴运动，运动方程为x=2t2+6(SI)，则质点的加速度大小为( )

两个质量相同的质点，初速度相同，任意瞬时的切向加速度大小也相同，各沿不同的光滑曲线运动。下述说法正确的是（）。

一点作曲线运动，开始时速度V0=10m/s，某瞬时切向加速度a1＝4m/s2，则2s末该点速度大小为（）

下述各种情况下，动点的全加速度a、切向加速度at和法向加速度an三个矢量之间正确的是（）。（1）点沿曲线作匀速运动。（2）点沿曲线运动，在该瞬时其速度为零。（3）点沿直线作变速运动。（4）点沿曲线作变速运动。

某一瞬时,作平面运动的平面图形内任意两点的加速度在此两点连线上投影相等,则可以断定该瞬时平面图形( )。

甲乙两物体的质量为m甲＝4m乙，在大小相等的拉力作用下由静止沿光滑水平面运动，经过相等的位移之后，甲乙两物体的动能之比为____，两物体的速度之比为____．

一物体做匀变速直线运动，初速度大小为15m/s，方向向东，第5s末的速度大小为10m/s，方向向西，则物体开始向西运动的时刻为：（）

一、教材阅读 1、平均速度与瞬时速度的区别与联系 (1)平均速度是运动物体在某一段时间内位移的平均值,即用时间除位移得到,(2)瞬时速度是物体在某一时间点的速度, 当时间段越来越的过程中,平均速度就越来越接近一个数值,这个数值就是瞬时速度, 可以说,瞬时速度是平均速度在时间间隔无限趋于时的 “飞跃”. 2 、求瞬时速度的步骤设物体运动方程为 s = f ( t ) , 则求物体在 t 时刻瞬时速度的步骤为: (1) 从 t 到 t + d 这段时间内的平均速度为 d ( f(t+d)-f(t) ) , 其中 f ( t + d ) - f ( t ) 称为位移的增量; (2) 对上式化简 , 并令 d 趋于 , 得到极限数值即为物体在 t 时刻的瞬速度. 3、曲线的割线与切线的区别与联系 (1) 曲线的割线的斜率反映了曲线在这一区上上升或下降的变化趋势 ,刻画了曲线在这一区间升降的程度, (2)曲线的切线是割线与曲线的一交点向另一交点逼时的一种极限状态,它实现了由割线向切线质的飞跃. 4、求曲线上点 P 处切线斜率的方法设 P ( u , f ( u )) 是函数 y = f ( x ) 的曲线上的任一点,则求点 P 处切线斜率的方法是: (1) 在曲线上取不同于 P 的点 Q ( u + d , f ( u + d )) , 计算直线 PQ 的斜率 k ( u , d ) = . (2) 在所求得的 PQ 的斜率的表达式 k ( u , d ) 中让 d 趋于 0 , 如果 k ( u , d ) 趋于确的数值 k ( u ) ,则就是曲线在 P 处的切线斜率. 二、基础作业: 1、已知一物体作自由落体运动 , s= 2 ( 1 ) gt 2 ( 位移单位: m , 时间单位: s , g=9.8 m/s 2 ). (1) 计算 t 从 3 s 到 3.1 s,3.01 s,3.001 s 各段时间内平均速度; (2) 求 t = 3 s 时的瞬时速度. 2、已知点 A ( x 1 , y 1 ) , B ( x 2 , y 2 ) 为函数 y = x 3 曲线上两不同点.

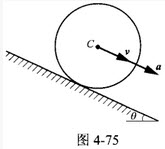
相关题目: 两个液流只要在相应点的速度和加速度的大小成比例，则两个液流就是运动相似的。; 某瞬时若平面图形上各点的加速度方向都指向同一点，则可知此瞬时平面图形的角速度ω和角加速度a为（　　）。[2012年真题]; 质点沿半径的圆周运动,角速度,角加速度,则其速度和加速度的大小分别是:( ); 运动质点在某瞬时位于位矢¯r=（x，y）端点处，其速度大小为; 运动质点在某瞬时位于位矢端点处ˉπ=（x，y），其速度大小为; 半径为R、质量为m的均质圆轮沿斜面作纯滚动如图4-75所示。已知轮心C的速度为ν、加速度为a，则该轮的动能为（）。; 点M沿平面曲线运动，在某瞬时，速度大小ν=6m/s，加速度大小a=8m/s2，两者之间的夹角为30°，如图4-38所示，则点M所在之处的轨迹曲率半径ρ为（）m。; 图4-44所示机构由杆O1A、O2B和三角板ABC组成。已知：杆O1A转动的角速度为ω，O1A=O2B=r，AC=h，O1O2=AB，则图示瞬时点C速度νC的大小和方向为（）。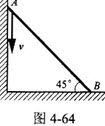; 杆AB长为ι，质量为m，图4-64所示瞬时点A处的速度为ν，则杆AB动量的大小为（）。; 对于平移刚体，任一瞬时，各点速度大小相等而方向可以不同。; 点作直线运动，已知某瞬时加速度为a=-2m／s^s，t=1s时速度为v₁=2m／s，则t=2s时，该点的速度大小为（）; （2008）点沿轨迹已知的平面曲线运动时，其速度大小不变，加速度α应为：（）; 平面运动刚体在某瞬时为瞬时平动时，其角速度ω和角加速度a是：（）; 某瞬时若平面图形上各点的加速度方向都指向同一点，则可知此瞬时平面图形的角速度ω和角加速度α为（）。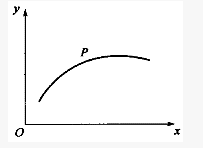; 图示瞬时，作平面运动图形上A、B两点的加速度相等，即a_A=a_b，则该瞬时平面图形的角速度ω与角加速度a分别是：（）; 刚体平面运动时，刚体上任一点的轨迹（）平面曲线；刚体平动时，刚体上任一点的轨迹（）空间曲线。; 刚体平面运动时，刚体上任一点的轨迹（）平面曲线。; 点在某瞬时的速度为零，那么该瞬时点的加速度也为零。; 在某瞬时一动点的法向加速度等于零，而其切向加速度不等于零，该点是作直线运动还是作曲线运动？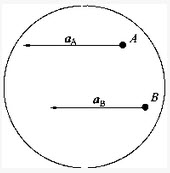（）; 下述各种情况下，动点的全加速度a、切向加速度a_t和法向加速度a_n三个矢量之间正确的是（）。
（1）点沿曲线作匀速运动。
（2）点沿曲线运动，在该瞬时其速度为零。
（3）点沿直线作变速运动。
（4）点沿曲线作变速运动。

广告位招租WX:84302438

题库考试答案搜索网

免费的网站请分享给朋友吧