无内热源，常物性二维导热物体在某一瞬时的温度分布为t＝2y2cosx。试说明该导热物体在x＝0，y=1处的温度是随时间增加逐渐升高，还是逐渐降低。 -题库考试答案搜索网

无内热源，常物性二维导热物体在某一瞬时的温度分布为t＝2y²cosx。试说明该导热物体在x＝0，y=1处的温度是随时间增加逐渐升高，还是逐渐降低。

问答题

2021-12-26 18:33

查看答案

正确答案

试题解析

标签：传热学物理学

感兴趣题目

简述导热系数，表面传热系数和传热系数之间的区别。

三层平壁导热的传热系数为各层平壁传热系数之和

对于一个二维、无内热源、常物性的稳态导热问题，其中任意一个内节点（i，j）的节点方程式应为（　　）。

简述Bi和Fo准则的物理意义Bi→0和Bi→∞时，一维平板非稳态导热温度分布的特点（用图形表示）。

在导热的基本定律--傅立叶定律中，有一个参数λ-导热系数。它的物理意义为：当壁厚为1m，温度差为1℃时，单位时间内通过单位面积的导热量。由此我们得知，物体的导热系数越大，表明该物体导热能力（）。

在导热的基本定律--傅立叶定律中，有一个参数λ-导热系数。它的物理意义为：当壁厚为1m，温度差为1℃时，单位时间内通过单位面积的导热量。由此我们得知，物体的导热系数越大，表明该物体导热能力()。

现在值是指现在某一时刻一次支付或收入的金额，也可以是未来某一时刻的资金换算到现在时刻的值，还可以是资金在某一规定时间t的值，称为t年的现值.一般用字母P表示，简称现值.（）

设有如图所示的一个无内热源的二维稳态导热物体，其上凹面、下表面分别维持在均匀温度t1和t2，其余表面绝热。

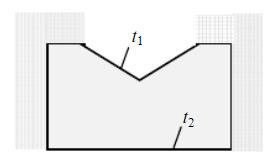说明材料的导热系数是否对温度分布有影响。

一块无限太平板，单侧表面积为A，初温为t0，一侧表面受温度为t∞，表面传热系数为h的气流冷却，另一侧受到恒定热流密度qw的加热，内部热阻可以忽略，试列出物体内部的温度随时间变化的微分方程式并求解之。设其他几何参数及物性参数已知。

设某单层平壁的导热系数为λ=λ0（1+bt），则壁内温度分布线的形状为（）。

一、教材阅读 1、平均速度与瞬时速度的区别与联系 (1)平均速度是运动物体在某一段时间内位移的平均值,即用时间除位移得到,(2)瞬时速度是物体在某一时间点的速度, 当时间段越来越的过程中,平均速度就越来越接近一个数值,这个数值就是瞬时速度, 可以说,瞬时速度是平均速度在时间间隔无限趋于时的 “飞跃”. 2 、求瞬时速度的步骤设物体运动方程为 s = f ( t ) , 则求物体在 t 时刻瞬时速度的步骤为: (1) 从 t 到 t + d 这段时间内的平均速度为 d ( f(t+d)-f(t) ) , 其中 f ( t + d ) - f ( t ) 称为位移的增量; (2) 对上式化简 , 并令 d 趋于 , 得到极限数值即为物体在 t 时刻的瞬速度. 3、曲线的割线与切线的区别与联系 (1) 曲线的割线的斜率反映了曲线在这一区上上升或下降的变化趋势 ,刻画了曲线在这一区间升降的程度, (2)曲线的切线是割线与曲线的一交点向另一交点逼时的一种极限状态,它实现了由割线向切线质的飞跃. 4、求曲线上点 P 处切线斜率的方法设 P ( u , f ( u )) 是函数 y = f ( x ) 的曲线上的任一点,则求点 P 处切线斜率的方法是: (1) 在曲线上取不同于 P 的点 Q ( u + d , f ( u + d )) , 计算直线 PQ 的斜率 k ( u , d ) = . (2) 在所求得的 PQ 的斜率的表达式 k ( u , d ) 中让 d 趋于 0 , 如果 k ( u , d ) 趋于确的数值 k ( u ) ,则就是曲线在 P 处的切线斜率. 二、基础作业: 1、已知一物体作自由落体运动 , s= 2 ( 1 ) gt 2 ( 位移单位: m , 时间单位: s , g=9.8 m/s 2 ). (1) 计算 t 从 3 s 到 3.1 s,3.01 s,3.001 s 各段时间内平均速度; (2) 求 t = 3 s 时的瞬时速度. 2、已知点 A ( x 1 , y 1 ) , B ( x 2 , y 2 ) 为函数 y = x 3 曲线上两不同点.

以下哪些命令可以将二维图形转化为三维物体（　　）。

相关题目: 设某单层平壁的导热系数为λ=λ0(1+bt),则壁内温度分布线的形状为( ).; 层析成像技术是利用在物体外部观测得到的物理场量，通过特殊的数字处理技术，重现物体内部物性或状态参数的分布图像，从而解决有关的工程技术问题，其所用的观测方式（）; 一物体做变速直线运动,已知路程与时间的函数关系式为S=t3+10则物体在时刻t=3时的瞬时速度为(); 一直径为d。，单位体积内热源的生成热Φ的实心长圆柱体，向温度为t∞的流体散热，表面传热系数为h。试列出圆柱体中稳态温度场的微分方程式及定解条件。; 无内热源，常物性二维导热物体在某一瞬时的温度分布为t＝2y²cosx。试说明该导热物体在x＝0，y=1处的温度是随时间增加逐渐升高，还是逐渐降低。; 在加热或冷却过程中，若物体内温度分布均匀，在任意时刻都可用一个温度来代表整个物体的温度，则该物体称为（）; 在某列管换热器中，若换热器的传热量为225kW，传热系数为603W/（m²/℃），两流体的传热平均推动力为23.6℃，则该换热器的传热面积为（）m²。; 通过长圆筒壁导热时，圆筒壁内的温度呈（）分布规律.; 辐射传热物体的固有特性，自然界中的一切物体均以辐射方式向空间传递能量，物体自身温度越（），辐射传递出的能量也越多。辐射传热的特点是不需要（），只有当物体的温度降到绝对零度时，物体的辐射传热现象才告终止。; 已知某一正弦交流电流，在t=0．1s时，其瞬时值为2A，初相角为60°，有效值I为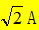
，求此电流的周期T和频率f。; 在某一瞬时，物体在力矩作用下，则有（）。; 传导又称热传导，简称导热，其机理是当物体的内部或两个（）的物体之间存在（）差异时，物体中温度（）部分的分子因振动而与相邻分子碰撞，并将能量的一部分传给后者，为此，（）就从物体的温度较高部分传到温度较低部分或从一个温度较高的物体传递给（）的温度较低的物体。; 温度是表示物体冷热程度的物理量，只能通过物体随温度变化的某些特性来间接测量。; 点在某瞬时的速度为零，那么该瞬时点的加速度也为零。; 一物体做变速直线运动，它的速度函数是v=2t+1，t=1时该物体的瞬时加速度为（）。; 一物体做变速直线运动，它的位置函数是s=，t=2时该物体的瞬时速度为4。; 在某一瞬时压强相对于无声波时的压强变化称为（），其单位是（）; 在某一瞬时，从动件运动规律不变的情况下，要减小凸轮的基圆半径rb，则压力角α（）; 无内热源，常物性二维导热物体在某一瞬时的温度分布为t＝2y 2cosx。试说明该导热物体在x＝0，y=1处的温度是随时间增加逐渐升高，还是逐渐降低。; 温度场是指某一时刻物体内的温度分布，它是（）的函数。

广告位招租WX:84302438

题库考试答案搜索网

免费的网站请分享给朋友吧