已知曲线y=f(x)上各点处的切线斜率为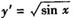 ,则曲线从x=0到x=π/2的长度s可表达成().
,则曲线从x=0到x=π/2的长度s可表达成().
设曲线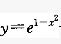 与直线x=-1的交点为为p,曲线在点p处的切线方程是:()
与直线x=-1的交点为为p,曲线在点p处的切线方程是:()
已知曲线y=f(x)上各点处的切线斜率为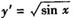 ,则曲线从x=0到x=π/2的长度s可表达成().
,则曲线从x=0到x=π/2的长度s可表达成().
若f(x)为可导的偶函数,则曲线y=f(x)在其上任意一点(x,y)和点(-x,y)处的切线斜率( )。
设周期函数f(x)在(-∞,+∞)内可导,周期为3,又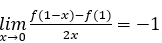 ,则曲线在点(4,f(4))处的切线斜率为( )。
,则曲线在点(4,f(4))处的切线斜率为( )。

已知函数f(x)=x-alnx(a∈R)
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值。
计算题:若消费者张某的收入为270元,他在商品X和Y的无差异曲线上的斜率为dY/dX=-20/Y的点上实现均衡。已知商品X和商品Y的价格分别为PX=2,PY=5,那么此时张某将消费X和Y各多少?
免费的网站请分享给朋友吧