面积为S、质量为m的薄板连接于弹簧下端,在粘性流体中振动,如下图所示。作用于薄板的阻尼力为F d=μ2Sv,2S为薄板总面积,v为速度。若测得薄板无阻尼自由振动的周期为T 0,在粘性流体中自由振动的周期为T d。求系数μ。 

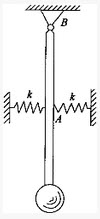
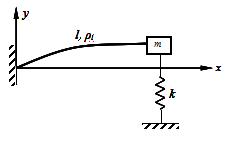
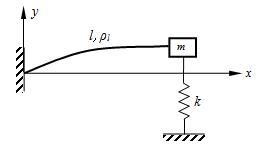
什长力L,一端与重力的大小为P的小球刚结,另一端用铰支座支承于B,在杆的中点A的两边各连接一刚性系数为k的弹簧,如图所示。若杆和弹簧的质量不计,小球可视为一质点,则该系统作微小摆动时的运动微分方程为()
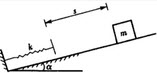
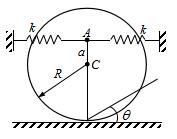
如图所示,在倾角为α的光滑斜面上置一刚性系数为k的弹簧,一质量为m的物体沿斜面下滑s距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率为()。
如图所示,在倾角为口的光滑斜面上置一弹性系数为k的弹簧,一质量为m的物块沿斜面下滑,距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率为()。



 系统发生共振。
系统发生共振。

 当估算围护结构风荷载时,方案a和方案b相同高度迎风面中点处单位面积风荷载比值,最接近于()。提示:按《建筑结构荷载规范》(GB50009-2012)解题。
当估算围护结构风荷载时,方案a和方案b相同高度迎风面中点处单位面积风荷载比值,最接近于()。提示:按《建筑结构荷载规范》(GB50009-2012)解题。

某矩形框筒,平面尺寸如下图所示,总高度102m,承受水平力q=20kN/m,框筒截面可简化成双槽形截面,该截面如下图所示。角柱为L形、截面面积A3=6.41m2、形心坐标y=0.90m。槽形截面惯性矩为3056.5m4。计算图中底层3号柱所受的轴力N3最接近于()kN。平面图(单位:m)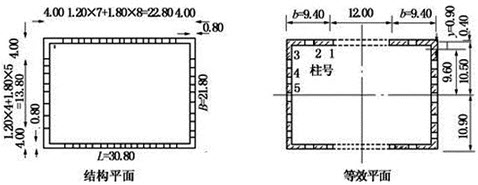
图示在倾角为a的光滑斜面上置一弹性系数为k的弹簧,一质量为m的物块沿斜面下滑s距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率应为()
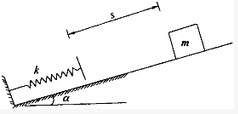
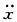 +kx=0,则描述运动的坐标ox的坐标原点应为()。
+kx=0,则描述运动的坐标ox的坐标原点应为()。 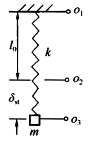
免费的网站请分享给朋友吧