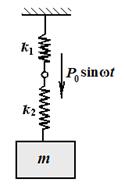
轻弹簧与物体的连接如图所示,物体质量为m,弹簧的劲度系数为k 1和k 2,支承面为理想光滑面,求系统振动的固有频率。 

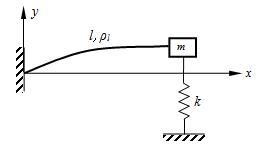
什长力L,一端与重力的大小为P的小球刚结,另一端用铰支座支承于B,在杆的中点A的两边各连接一刚性系数为k的弹簧,如图所示。若杆和弹簧的质量不计,小球可视为一质点,则该系统作微小摆动时的运动微分方程为()
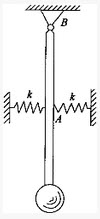
如图所示,与水平面夹角为300的固定斜面上有一质量m=1.0kg的物体。细绳的一端与物体相连,另一端经摩擦不计的定滑轮与固定的弹簧秤相连。物体静止在斜面上,弹簧秤的示数为4.9N。关于物体受力的判断(取g=9.8m/s2),下列说法正确的是()。
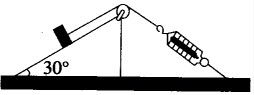
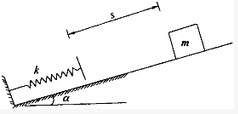
如图所示,在倾角为α的光滑斜面上置一刚性系数为k的弹簧,一质量为m的物体沿斜面下滑s距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率为()。
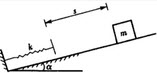
如图所示,在倾角为口的光滑斜面上置一弹性系数为k的弹簧,一质量为m的物块沿斜面下滑,距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率为()。

将质量为m的物体在空气中竖直上抛,初速度为V0,若空气阻力与物体的速度v(t)(t是时间)成正比,比例系数为K,g为重心加速度。则下列哪个方程是v(t)所满足的微分方程()?



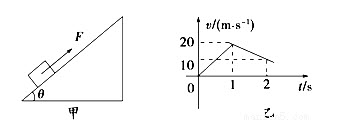
如图甲,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,在t1=1s时撤去拉力,物体运动的部分vt图象如图乙所示.重力加速度g取10m/s2.sin37°=0.6,cos37°=0.8.试求:
(1)拉力F的大小.
(2)t=5s时物体的速度v的大小.
图示在倾角为a的光滑斜面上置一弹性系数为k的弹簧,一质量为m的物块沿斜面下滑s距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率应为()
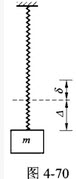
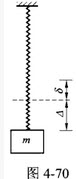
如图4-70所示,常数为k的弹簧下挂一质量为m的物体,若物体从静平衡位置(设静伸长为δ)下降△距离,则弹性力所做的功为()。
如图所示,质量分别为m1、m2的两个物体通过轻弹簧连接,在力F的作用下一起沿水平方向做匀速直线运动(m1在地面,m2在空中),力F与水平方向成θ角,m1所受支持力N、摩擦力f正确的是()。

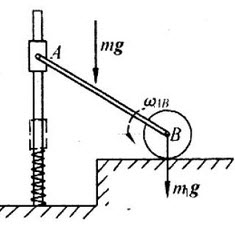
已知均质杆AB的质量m=4kg,长l=600mm,均匀圆盘B的质量为6kg,半径为r=600mm,作纯滚动。弹簧刚度为k=2N/mm,不计套筒A及弹簧的质量。连杆在与水平面成30º角时无初速释放。求(1)当AB杆达水平位置而接触弹簧时,圆盘与连杆的角速度;(2)弹簧的最大压缩量δmax
两个质量不同的质点用弹簧相连,平放在光滑的水平面上。弹簧刚度系数为k,弹簧原长为l0。现将两质点拉开,使弹簧拉长到l后无初速地释放。当弹簧恢复到原长瞬时:两个质点的速度都()。
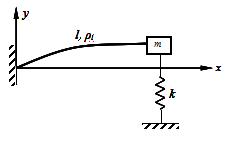
免费的网站请分享给朋友吧