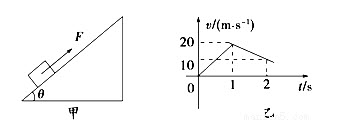
如图甲,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,在t1=1s时撤去拉力,物体运动的部分vt图象如图乙所示.重力加速度g取10m/s2.sin37°=0.6,cos37°=0.8.试求:
(1)拉力F的大小.
(2)t=5s时物体的速度v的大小.
分析:
(1)根据速度时间图线求出物体匀加速直线运动和匀减速直线运动的加速度大小,对匀加速和匀减速阶段分别运用牛顿第二定律求出拉力F的大小和动摩擦因数的大小.
(2)根据速度时间公式求出物体上滑到最高点所需的时间,根据牛顿第二定律求出下滑的加速度,从而得出t=5s时物体的速度v的大小.
解:
(1)设力F作用时物体加速度为a1,对物体进行受力分析,由牛顿第二定律可知
F-mgsinθ-μmgcosθ=ma1
撤去力后,由牛顿第二定律有mgsinθ+μmgcosθ=ma2,
根据图象可知:a1=20m/s2,a2=10m/s2,
代入解得F=30N,μ=0.5.
(2)设撤去力后物体运动到最高点所需时间为t2,v1=a2t2,
解得t2=2s.
则物体沿着斜面下滑的时间为t3=t-t1-t2=2s
设下滑加速度为a3,由牛顿第二定律mgsinθ-μmgcosθ=ma3,
解得a3=2 m/s2
则t=5 s时速度v=a3t3=4m/s.
答:
(1)拉力F的大小为30N.
(2)t=5s时物体的速度v的大小为4m/s.
点评:本题考查牛顿第二定律和运动学公式的综合,注意物体匀减速上滑的加速度大小和返回做匀加速直线运动的加速度大小不等.

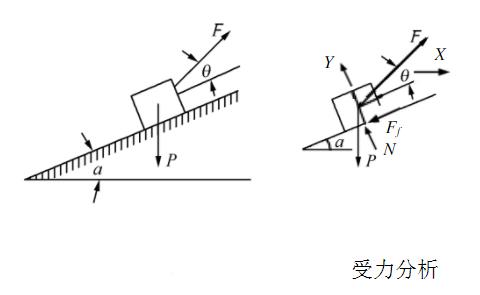


如图所示,将质量为m的滑块放在倾角为θ的固定斜面上,滑块与斜面之间的动摩擦因数为υ。若滑块与斜面之间的最大静摩擦力和滑动摩擦力大小相等,重力加速度为g,则()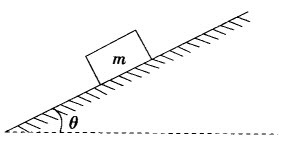
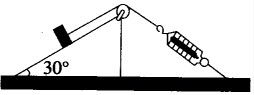
如图所示,与水平面夹角为300的固定斜面上有一质量m=1.0kg的物体。细绳的一端与物体相连,另一端经摩擦不计的定滑轮与固定的弹簧秤相连。物体静止在斜面上,弹簧秤的示数为4.9N。关于物体受力的判断(取g=9.8m/s2),下列说法正确的是()。
如图所示,在倾角为α的光滑斜面上置一刚性系数为k的弹簧,一质量为m的物体沿斜面下滑s距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率为()。

如图甲,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,在t1=1s时撤去拉力,物体运动的部分vt图象如图乙所示.重力加速度g取10m/s2.sin37°=0.6,cos37°=0.8.试求:
(1)拉力F的大小.
(2)t=5s时物体的速度v的大小.

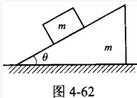
如图4-62所示质量为m的三角形物块,其倾斜角为θ,可在光滑的水平地面上运动。质量为m的矩形物块又沿斜面运动。两块间也是光滑的。该系统的动力学特征(动量、动量矩、机械能)有守恒情形的数量为()。
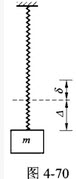
如图4-70所示,常数为k的弹簧下挂一质量为m的物体,若物体从静平衡位置(设静伸长为δ)下降△距离,则弹性力所做的功为()。
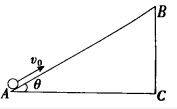
如图所示,长为L、倾角为θ的光滑绝缘斜面处于场强方向平行于纸面的电场中,一电荷量为q,质量为m的带正电小球,以初速度υ由斜面底端的A点开始沿斜面上滑,到达斜面顶端B点时速仍为υ,下列判断正确的是()
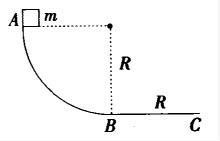
如图所示为用同样材料制成的一个轨道,AB段为1/4圆弧,半径为R,水平的BC段长为R,一小物体质量为m,与轨道间的动摩擦因数为μ,当它从轨道顶端A由静止下滑时恰好运动到C点静止,那么物体在AB段克服摩擦力做的功为()。
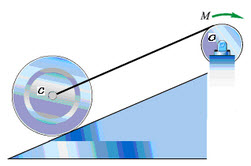
已知:轮O的半径为R1,质量为m1,质量分布在轮缘上;均质轮C的半径为R2,质量为m2,与斜面纯滚动,初始静止。斜面倾角为θ,轮O受到常力偶M驱动。求:轮心C走过路程s时的速度和加速度。
一质量为G的物体用绳子吊在空中并保持静止。
问:1:该物体处于何种运动状态?2:该物体受到那些力的作用3:这些力的等效合力为多少?
免费的网站请分享给朋友吧