

 系统发生共振。
系统发生共振。

 ω等于固有频率ω n的一半。
ω等于固有频率ω n的一半。
计算透射系数K
知:V1=2600m/s,ρ1=2.2g/cm的立方,V2=5500m/s,ρ2=2.8g/cm的立方,
求:K=?

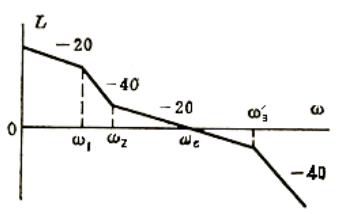
 若要求系统的相位裕量为45°,求K值。
若要求系统的相位裕量为45°,求K值。



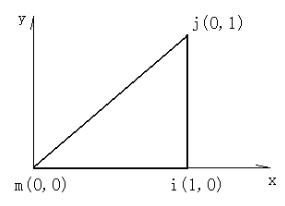 求单元刚度矩阵K。
求单元刚度矩阵K。
 求应力矩阵[S]。
求应力矩阵[S]。
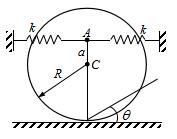
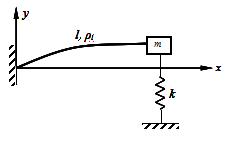
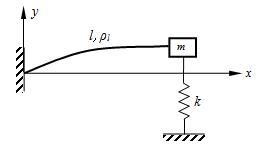
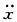 +kx=0,则描述运动的坐标ox的坐标原点应为()。
+kx=0,则描述运动的坐标ox的坐标原点应为()。 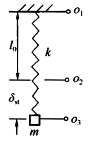
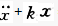 +=0,则描述运动的坐标o
+=0,则描述运动的坐标o 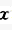 的坐标原点应为()。
的坐标原点应为()。 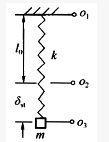
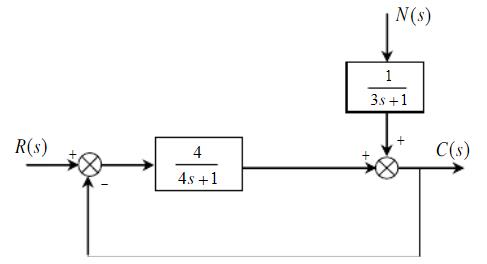
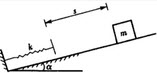
如图所示,在倾角为α的光滑斜面上置一刚性系数为k的弹簧,一质量为m的物体沿斜面下滑s距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率为()。
免费的网站请分享给朋友吧