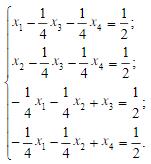（a）求解此方程组的雅可比迭代法的迭代矩阵B 0的谱半径； （b）求解此方程组的高斯－塞德尔迭代法的迭代矩阵的谱半径； （c）考察解此方程组的雅可比迭代法及高斯－塞德尔迭代法的收敛性。
。式中，u和y分别为系统输入和输出量。试列写可控标准型（即矩阵A为友矩阵）及可观测标准型（即矩阵A为友矩阵转置）状态空间表达式。
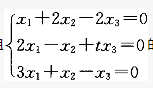的解，则t等于：（）
的解，则t等于：（）
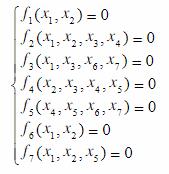请用Sargent & Westerberg法将方程组分解为维数较小的子方程组，并用组合节点（拟节点）表示出子方程组的计算顺序。
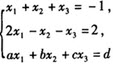有两个不同的解，则增广矩阵的秩等于（）．
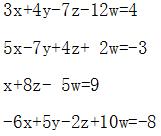（1）求系数矩阵的秩； （2）求出方程组的解。
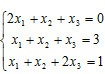
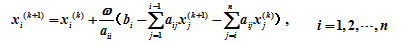（1）试导出其矩阵迭代格式及迭代矩阵； （2）证明当A是严格对角占优阵， 
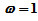时此迭代格式收敛。
分别对a进行特征值分解、奇异值分解、LU分解、QR分解。
设
与
分别代表非齐次线性方程组
的系数矩阵和增广矩阵，若这个方程组有解，则（ ）．
设与分别代表非齐次线性方程组的系数矩阵和增广矩阵，若这个方程组无解，则（ ）．
对线性方程组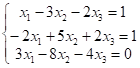
的增广矩阵做初等行变换可得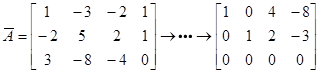
则该方程组的一般解为（ ），其中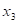
是自由未知量．
对线性方程组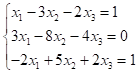
的增广矩阵做初等行变换可得
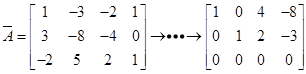则该方程组的一般解为（ ），其中
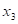是自由未知量．
对线性方程组
的增广矩阵做初等行变换可得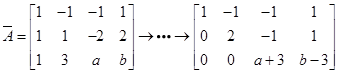 
则当（ ）时，该方程组有无穷多解．
对线性方程组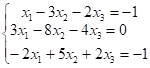
的增广矩阵做初等行变换可得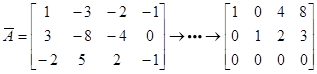 
则该方程组的一般解为（ ），其中
是自由未知量．
对线性方程组
的增广矩阵做初等行变换可得 
则当（ ）时，该方程组无解．
对线性方程组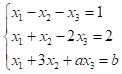
的增广矩阵做初等行变换可得 
则当（ ）时，该方程组有唯一解．
若线性方程组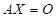
只有零解，则线性方程组
（ ）．
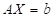已知矩阵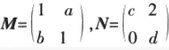
，且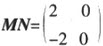
。
（Ⅰ）求实数a、b、c、d的值；（Ⅱ）求直线y=3x在矩阵M所对应的线性变换作用下的像的方程。
一项病例对照研究数据如下，其OR值为（）
设B是三阶非零矩阵，已知B的每一列都是方程组
的解，则t等于：（）
设A为矩阵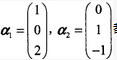
，都是齐次线性方程组Ax=0的解，则矩阵A为（）。
已知非齐次线性方程组
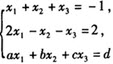有两个不同的解，则增广矩阵的秩等于（）．
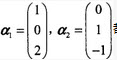，都是齐次线性方程组Ax=0的解，则矩阵A为（）。
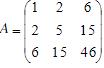，然后求解该方程组 
。
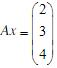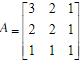，然后求解该方程组 
。
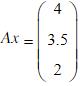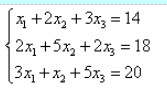
免费的网站请分享给朋友吧
