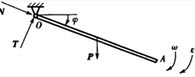
如图所示,均质杆OA,重为P,长为2l,绕过O端的水平轴在铅直面内转动,转到角时,有角速度ω和角加速度ε,则此时铰链O处约束力T和N为()。
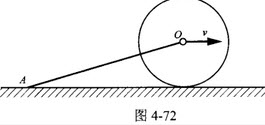
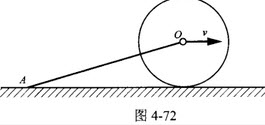
如图4-72所示,质量为m1的均质杆OA,一端铰接在质量为m2的均质圆盘中心,另一端放在水平面上,圆盘在地面上作纯滚动。圆心速度为ν,则系统的动能为()。
如图所示,均质圆盘重为W,半径为R,绳子绕过圆盘,两端各挂重为Q和P的物块,绳与盘之间无相对滑动,且不计绳重,则圆盘的角加速度为()。

杆OA绕固定轴O转动,长为 。某瞬时杆端A点的加速度为
。某瞬时杆端A点的加速度为 ,如图所示。则该瞬时OA杆的角速度及角加速度为()。
,如图所示。则该瞬时OA杆的角速度及角加速度为()。


质量为m,长为2 的均质细杆初始位于水平位置,如图所示。A端脱落后,杆绕轴B转动,当杆转到铅垂位置时,AB杆角加速度的大小为()。
的均质细杆初始位于水平位置,如图所示。A端脱落后,杆绕轴B转动,当杆转到铅垂位置时,AB杆角加速度的大小为()。

如图所示,两均质杆AC和BC各重P,长均为l,在C处以铰链连接,并置于光滑水平面上。C点的初始高度为h,两杆从静止开始在铅直面内落下,则铰链C到达地面C’时的速度vC为()。

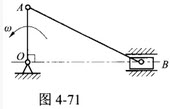
如图4-71所示曲柄连杆机构中,OA=r,AB=2r,OA、AB及滑块B质量均为m,曲柄以ω的角速度绕O轴转动,则此时系统的动能为()。



A campus emergency ______ occur at any time of the day or night, weekend, or holiday, with little or no warning.
如图所示,板长为Z,水平地置于直角槽内,已知板的A端与槽面间的摩擦系数为f,B端摩擦不计,若不计板重,则重为P的人站在板上能使板保持水平,其位置应为()。
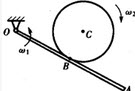
图示杆OA以角速度ψ1绕O轴旋转,轮C相对杆以角速度ω2在杆上滚动。轮半径为R,杆长为2l,此瞬时OB=BA。若以轮心C为动点,动系固结在OA杆上,则C点的牵连速度vE为()。
质量为m1,半径为r的均质圆盘上,沿水平直径方向焊接一长为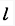 ,质量为m2的均质杆AB。整个物体绕圆盘中心O以角速度w转动,该物体系统的总动量的大小为()。
,质量为m2的均质杆AB。整个物体绕圆盘中心O以角速度w转动,该物体系统的总动量的大小为()。
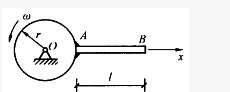
质量为m,长度为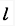 的均质杆铰接于O点,A端固结一质量为m的质点如图示。当OA杆以角速度w绕O轴转动时,系统对轴O的动量矩的大小为()。
的均质杆铰接于O点,A端固结一质量为m的质点如图示。当OA杆以角速度w绕O轴转动时,系统对轴O的动量矩的大小为()。
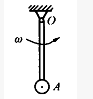
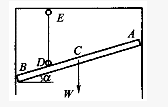
(2011)均质杆AB长为ι,重为W,受到如图所示的约束,绳索ED处于铅垂位置,A、B两处为光滑接触,杆的倾角为α,又CD=ι/4,则A、B两处对杆作用的约束力大小关系为:()
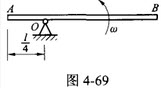
均质细直杆AB长为ι,质量为m,以匀角速度ω绕O轴转动,如图4-69所示,则AB杆的动能为()。
一端固定一端自由的细长(大柔度)压杆,长为L(如图a)所示,当杆的长度减小一半时(如图b)所示,其临界荷载Fcr比原来增加:()

如图a所示为()
如图b所示为()
如图d所示为()
如图f所示为()
如图g所示为()
]如图所示,均质圆柱A、B重均为P,半径均为r,绳子一端绕在绕O轴转动的A圆柱上,另一端绕在B圆柱上。若不计摩擦,则B落下时其质心C的加速度aC为()。

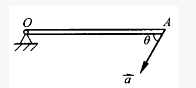
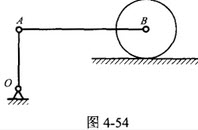
如图4-54所示,平面机构在图示位置时,杆AB水平而杆OA铅直,若B点的速度νB≠0,加速度aB=0。则此瞬时杆OA的角速度、角加速度分别为()。
长为L,质量为m1的均质杆OA的A端焊接一个半径为r,质量为m2的均质圆盘,该组合物体绕O轴转动的角速度w,则系统对O轴的动量矩H。()。
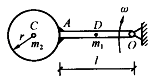
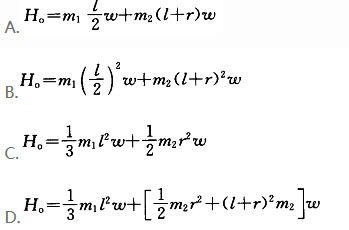
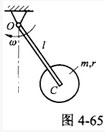
如图4-65所示,忽略质量的细杆OC=ι,其端部固结均质圆盘。杆上点C为圆盘圆心。盘质量为m。半径为r。系统以角速度ω绕轴O转动。系统的动能是()。
均质直角曲杆OAB的单位长度质量为ρ,OA=AB=2l,图示瞬时以角速度ω、角加速度a绕轴O转动,该瞬时此曲杆对O轴的动量矩的大小为:()
如图所示,均质杆OA,重为P,长为l,可在铅直平面内绕水平固定轴O转动。杆在图示铅直位置时静止,欲使杆转到水平位置,则至少要给杆以角速度ω为()。

如图所示,均质杆OA,重为P,长为2l,绕过O端的水平轴在铅直面内转动,转到角时,有角速度ω和角加速度ε,则此时铰链O处约束力T和N为()。

已知:如图所示均质圆环半径为r,质量为m,其上焊接刚杆OA,杆长为r,质量也为m。用手扶住圆环使其在OA水平位置静止。设圆环与地面间为纯滚动。求:放手瞬时,圆环的角加速度,地面的摩擦力及法向约束力。
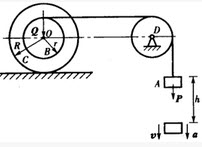
如图所示,物块A重为P,连在不计重量、不伸长的绳子上。绳子绕过定滑轮D并绕在鼓轮B上。当A下落时带动轮C沿水平直线轨道作纯滚动。鼓轮B的半径为r,C的半径为R,两轮固连,总重为Q,其对水平中心轴O的回转半径为ρ,轮D半径r,重不计,则物块A的加速度a为()。
免费的网站请分享给朋友吧