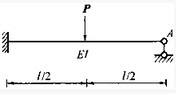
图中取A支座反力为力法的基本未知量X1（向上为正），则X1大小为：（） 
试求模糊集合R=A∩B∩C，S=A∪B∪C和T=A∪B∩C。
具有待定特解形式为y=A1x+A2+B1ex的微分方程是下列中哪个方程（）？
设二次函数f（x）=ax2+bx+c（a>O），方程f（x）-x=O的两个根x1，x2满足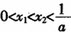
。
（1）当x∈（0，x1）时，证明x；
（2）设函数f（x）的图象关于直线x=x0对称，证明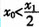
。
为样本均值，S2为样本方差，若μ为未知参数且σ为已知参数，下列随机变量中属于统计量的有（ ）。[2005年中级真题]
为样本均值，S2为样本方差，若μ为未知参数且σ为已知参数，下列随机变量中属于统计量的有（ ）。[2005年中级真题]
为样本均值，S2为样本方差，若μ为已知参数且σ为未知参数，下列随机变量中属于统计量的有（ ）。
某起高处坠落事故的事故树分析如图所示，T代表高处坠落事故，A代表安全带未起作用，B代表脚手架栏杆缺失，X1为安全带功能损失，X2为安全带未高挂抵用，X3为安全措施费用不到位，X4为脚手架栏杆强度不足，可能导致该起事故的原因有（ ）。
A．X1X3
B．X2X3
C．X1X2
D．X1X4
E．X2X4
[图1]
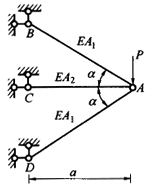
图示桁架取杆AC轴力（拉为正）为力法的基本未知量X1，则有：（）
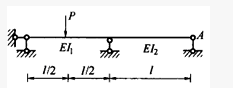
图示结构，若取梁B截面弯矩为力法的基本未知量Xl，当I2增大时，则X1绝对值的变化状况是：（）
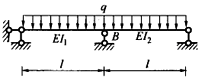
图中取A支座反力为力法的基本未知量X1，当I1增大时，柔度系数δ11的变化状况是：（）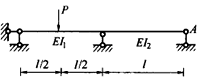
已知函数在x0处可导，且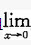
｛x／[f（x0-2x）-f（x0）]｝=1／4，则f′（x0）的值为：（）
没A是n*n常数矩阵（n>1），X是由未知数X1，X2，…，Xn组成的列向量，B是由常数b1，b2，…，bn组成的列向量，线性方程组AX=B有唯一解的充分必要条件不是（）。
设F1（x）与F2（x）分别为随机变量X1与X2的分布函数。为使F（x）=aF1（x）-bF2（x）成为某一随机变量的分布函数，则a与b分别是：（）
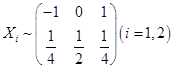，满足P{X1X2＝0}＝1，则P{X1＝X2}等于（ ）。
免费的网站请分享给朋友吧