设非齐次线性方程组Ax=b，其中A是m×n矩阵，则Ax=b有唯一解的充分必要条件是

设n阶矩阵A的伴随矩阵A*≠O，若ξ1，ξ2，ξ3，ξ4是非齐次方程组Ax=b的互不相同的解，则Ax=0的基础解系

设n阶矩阵A的伴随矩阵A*≠0，若ζ1，ζ2，ζ3，ζ4是非齐次方程组Ax=b的互不相等的解，则对应的齐次线性方程组Ax=0的基础解系______．

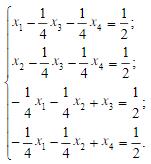设方程组 （a）求解此方程组的雅可比迭代法的迭代矩阵B ₀的谱半径； （b）求解此方程组的高斯－塞德尔迭代法的迭代矩阵的谱半径； （c）考察解此方程组的雅可比迭代法及高斯－塞德尔迭代法的收敛性。

设A为n阶方阵，若α是非齐次线性方程组Ax=b的解，β1，β2，…，βr是导出组Ax=0的基础解系，则下列结论正确的是

已知4元非齐次线性方程组Ax=b的系数矩阵的秩等于3，且η1，η2，η3是3个不同的解向量，则通解是（）．

解线性方程组Ax=b的高斯顺序消元法满足的充要条件为（）。

Jacobi迭代法解方程组Ax=b的必要条件是（）

试用“追赶法”解方程组Ax=b，其中

已知β1β2是非齐次方程组AX=b的两个不同的解，α1α2是其对应的齐次线性方程组的基础解系，k1、k2是任意常数，则方程组AX=b的通解必是（　　）.

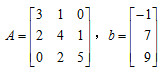
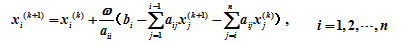已知求解线性方程组Ax=b的分量迭代格式 （1）试导出其矩阵迭代格式及迭代矩阵； （2）证明当A是严格对角占优阵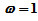， 时此迭代格式收敛。

设有方程组Ax=b，其中A为对称正定阵，迭代公式 试证明当0<ω<2/β时上述迭代法收敛（其中0<α≤λ（A）≤β）。