设有方程组Ax=b,其中A为对称正定阵,迭代公式  试证明当0<ω<2/β时上述迭代法收敛(其中0<α≤λ(A)≤β)。
试证明当0<ω<2/β时上述迭代法收敛(其中0<α≤λ(A)≤β)。
 , 当0<ω<2/β时,有-1<1-ωλ i<1,(i=1,2,...,n)
, 当0<ω<2/β时,有-1<1-ωλ i<1,(i=1,2,...,n) 设初值AX=6264H,CX=0004H,在执行下列程序段后AX=()
AND AX, AX
JZ DONE
SHL CX, 1
ROR AX, CL
DONE: OR AX, 1234H
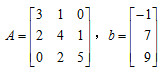
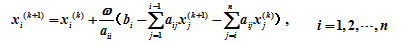 (1)试导出其矩阵迭代格式及迭代矩阵; (2)证明当A是严格对角占优阵,
(1)试导出其矩阵迭代格式及迭代矩阵; (2)证明当A是严格对角占优阵, 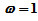 时此迭代格式收敛。
时此迭代格式收敛。
 试证明当0<ω<2/β时上述迭代法收敛(其中0<α≤λ(A)≤β)。
试证明当0<ω<2/β时上述迭代法收敛(其中0<α≤λ(A)≤β)。

设有齐次线性方程组Ax=0及Bx=0,其中A、B均为m×n矩阵,现有以下4个命题
①若Ax=0的解均是Bx=0的解,则rA≥rB;
②若rA≥rB,则Ax=0的解均是Bx=0的解;
③若Ax=0与Bx=0同解,则rA=rB;
④若rA=rB,则Ax=0与Bx=0同解。
以上命题中正确的是()。
设A为矩阵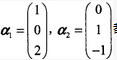 ,都是齐次线性方程组Ax=0的解,则矩阵A为()。
,都是齐次线性方程组Ax=0的解,则矩阵A为()。
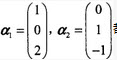 ,都是齐次线性方程组Ax=0的解,则矩阵A为()。
,都是齐次线性方程组Ax=0的解,则矩阵A为()。
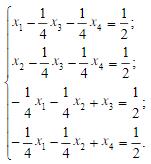 (a)求解此方程组的雅可比迭代法的迭代矩阵B 0的谱半径; (b)求解此方程组的高斯-塞德尔迭代法的迭代矩阵的谱半径; (c)考察解此方程组的雅可比迭代法及高斯-塞德尔迭代法的收敛性。
(a)求解此方程组的雅可比迭代法的迭代矩阵B 0的谱半径; (b)求解此方程组的高斯-塞德尔迭代法的迭代矩阵的谱半径; (c)考察解此方程组的雅可比迭代法及高斯-塞德尔迭代法的收敛性。
免费的网站请分享给朋友吧