设齐次线性方程组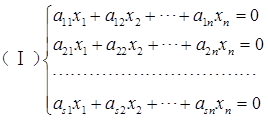
的系数矩阵的秩为r≠0。证明：（Ⅰ）的任意n－r个线性无关的解向量都是它的一个基础解系。
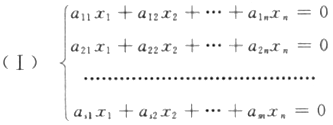的系数矩阵的秩为r≠0.
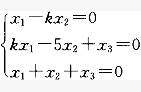，当方程组有非零解时，k值为：（）
，当方程组有非零解时，k值为：（）
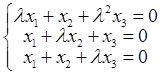的系数矩阵为A，存在方阵B≠0，使得AB＝0。
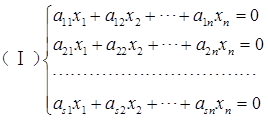的系数矩阵的秩为r≠0。证明：（Ⅰ）的任意n－r个线性无关的解向量都是它的一个基础解系。
的基础解系为（ ）。[2011年真题]
非齐次线性方程组
相容的充分必要条件是
．（ ）
当
1时，线性方程组
有无穷多解．（ ）
线性方程组
可能无解．（ ）
设
与
分别代表非齐次线性方程组
的系数矩阵和增广矩阵，若这个方程组有解，则（ ）．
若某个非齐次线性方程组相应的齐次线性方程组只有零解，则该线性方程组（ ）．
设与分别代表非齐次线性方程组的系数矩阵和增广矩阵，若这个方程组无解，则（ ）．
若
向量组线性无关，则齐次线性方程组
（ ）．
设线性方程组
的两个解
，则下列向量中（ ）一定是的解.
（2010）设齐次线性方程组
，当方程组有非零解时，k值为：（）
设A为矩阵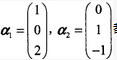
，都是齐次线性方程组Ax=0的解，则矩阵A为（）。
免费的网站请分享给朋友吧