质量为m,半径为r的定滑轮O上绕有细绳。依靠摩擦使绳在轮上不打滑,并带动滑轮转动。绳之两端均系质量m的物块A与B。块B放置的光滑斜面倾角为α,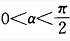 。假设定滑轮O的轴承光滑,当系统在两物块的重力作用下运动时,B与O间,A与O间的绳力FT1和FT2的大小有关系:()
。假设定滑轮O的轴承光滑,当系统在两物块的重力作用下运动时,B与O间,A与O间的绳力FT1和FT2的大小有关系:()
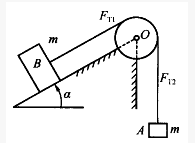


两重物的质量均为m,分别系在两软绳上。此两绳又分别绕在半径各为r与2r并固结在一起的两圆轮上。两圆轮构成之鼓轮的质量亦为m,对轴o的回转半径为ρ0。两重物中一铅垂悬挂,一置于光滑平面上。当系统在左重物的重力作用下运动时,鼓轮的角加速度α为()。
一普通完全井,半径r0=0.2m,含水层水头H=10m,渗透系数k=0.0006m/s,影响半径R=294m,抽水稳定后井中水深k=6m,此时该井的出水流量Q为()
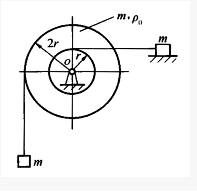
如图所示,倾角为θ的斜面体C置于水平面上,B置于斜面上,通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态,则()。
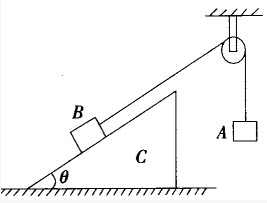
如图所示,与水平面夹角为300的固定斜面上有一质量m=1.0kg的物体。细绳的一端与物体相连,另一端经摩擦不计的定滑轮与固定的弹簧秤相连。物体静止在斜面上,弹簧秤的示数为4.9N。关于物体受力的判断(取g=9.8m/s2),下列说法正确的是()。

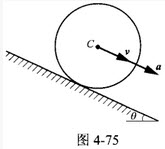
半径为R、质量为m的均质圆轮沿斜面作纯滚动如图4-75所示。已知轮心C的速度为ν、加速度为a,则该轮的动能为()。
质量为m,半径为r的定滑轮O上绕有细绳。依靠摩擦使绳在轮上不打滑,并带动滑轮转动。绳之两端均系质量m的物块A与B。块B放置的光滑斜面倾角为α,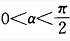 。假设定滑轮O的轴承光滑,当系统在两物块的重力作用下运动时,B与O间,A与O间的绳力FT1和FT2的大小有关系:()
。假设定滑轮O的轴承光滑,当系统在两物块的重力作用下运动时,B与O间,A与O间的绳力FT1和FT2的大小有关系:()

长为L,质量为m1的均质杆OA的A端焊接一个半径为r,质量为m2的均质圆盘,该组合物体绕O轴转动的角速度w,则系统对O轴的动量矩H。()。
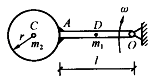
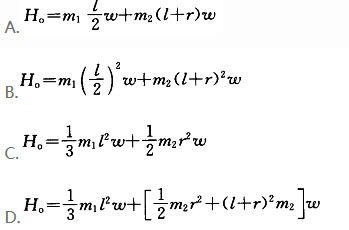
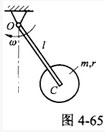
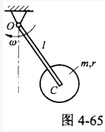
如图4-65所示,忽略质量的细杆OC=ι,其端部固结均质圆盘。杆上点C为圆盘圆心。盘质量为m。半径为r。系统以角速度ω绕轴O转动。系统的动能是()。
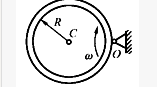
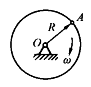
质量为2m,半径为R的偏心圆板可绕通过中心O的轴转动,偏心距OC=R/2。在OC连线上的A点固结一质量为m的质点,OA=R如图示。当板以角速度w绕轴O转动时,系统动量K的大小为()。(注:C为圆板的质心)。

]图中均质细圆环质量为m,半径为R,可绕环上O点并垂直于圆环平面的轴转动。已知角速度为w,顺时针转向,试求圆环对O轴的动量矩的大小及转向()
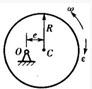
半径为R、质量为m的均质圆盘绕偏心轴O转动,偏心距e=R/2,图示瞬时转动角速度为ω,角加速度为ε,则该圆盘的惯性力系向O点简化的主矢量R1和主矩的大小为()。
图示均质圆轮,质量为m,半径为r,在铅垂图面内绕通过圆盘中心O的水平轴转动,角速度为w,角加速度为ε,此时将圆轮的惯性力系向O点简化,其惯性力主矢和惯性力主矩的大小分别为:()

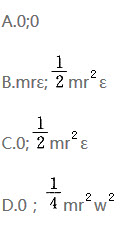
已知:轮O的半径为R1,质量为m1,质量分布在轮缘上;均质轮C的半径为R2,质量为m2,与斜面纯滚动,初始静止。斜面倾角为θ,轮O受到常力偶M驱动。求:轮心C走过路程s时的速度和加速度。
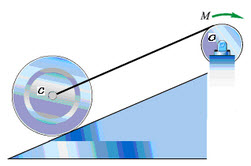
如图所示,物块A重为P,连在不计重量、不伸长的绳子上。绳子绕过定滑轮D并绕在鼓轮B上。当A下落时带动轮C沿水平直线轨道作纯滚动。鼓轮B的半径为r,C的半径为R,两轮固连,总重为Q,其对水平中心轴O的回转半径为ρ,轮D半径r,重不计,则物块A的加速度a为()。
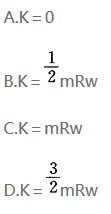
免费的网站请分享给朋友吧