曲线y=x3(x-4)既单增又向上凹的区间为()
设4/(1-x2)·f(x)=d/dx[f(x)]2,且f(0)=0,则f(x)等于:()
由曲线y=ex,y=e-2x及直线x=-1所围成图形的面积是:()

一项食盐量与高血压关联的病例对照研究资料,经分析后获如下数据:X2=12.26.P=0.01,OR=3.4,正确的研究结论是()
曲线y=(1/2)x2,x2+y2=8所围成图形的面积(上半平面部分)是:()

曲线y=x3(x-4)既单增又向上凹的区间为()
由曲线y=x2/2和直线x=1,x=2,y=-1围成的图形,绕直线y=-1旋转所得旋转体体积为:()
已知实数x、y满足:3(x3+y3+1)=(x-y+1)3,x2014+y2014=
曲线积分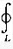 -2x3ydx+x2y2dy,其中L是由不等式x2+y2≥1及x2+y2≤2y所确定的区域D的正向边界,则其值为:()
-2x3ydx+x2y2dy,其中L是由不等式x2+y2≥1及x2+y2≤2y所确定的区域D的正向边界,则其值为:()
二元函数z=x3+y3-3x2+3y2-9x的极大值点是()
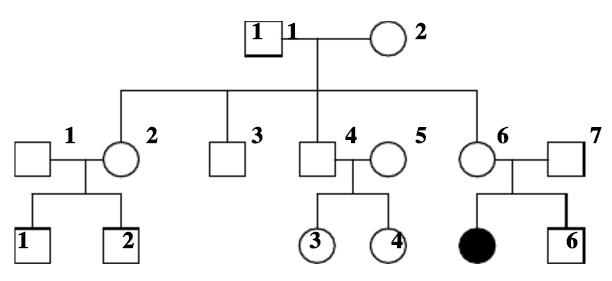 该单基因病最可能的遗传方式是?
该单基因病最可能的遗传方式是?
 该单基因病最可能的遗传方式是?
该单基因病最可能的遗传方式是?
免费的网站请分享给朋友吧