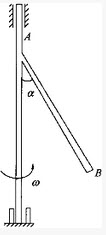
图示均质细杆AB长L，重力的大小为P，与铅垂轴固结成角a=30°，并以匀角速度ω转动，则惯性力系的合力的大小等于（）
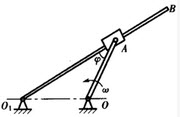
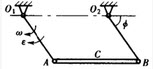
图示平面机构，曲柄OA长R，以角速度ω绕O轴转动，并通过杆端滑块A带动摆杆O1B绕O1轴转动。已知OA=OO1，图示位置=300，则此时杆O1B的角速度为（）。
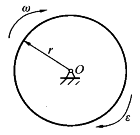
图示均质圆轮，质量为m，半径为r，在铅垂平面内绕通过圆盘中心O的水平轴转动，角速度为ε，此时将圆轮的惯性力系向O点简化，其惯性力系主矢和惯性力系主矩的大小分别为（）。
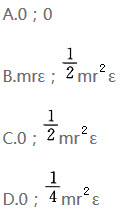
]图中均质细圆环质量为m，半径为R，可绕环上O点并垂直于圆环平面的轴转动。已知角速度为w，顺时针转向，试求圆环对O轴的动量矩的大小及转向（）
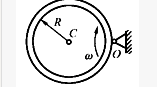
半径为R、质量为m的均质圆盘绕偏心轴O转动，偏心距e=R/2，图示瞬时转动角速度为ω，角加速度为ε，则该圆盘的惯性力系向O点简化的主矢量R1和主矩的大小为（）。
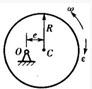
如图所示，均质杆OA，重为P，长为l，可在铅直平面内绕水平固定轴O转动。杆在图示铅直位置时静止，欲使杆转到水平位置，则至少要给杆以角速度ω为（）。
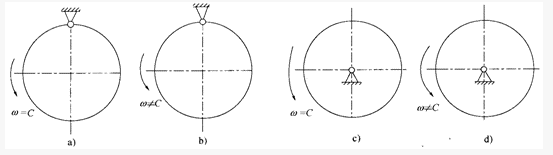
图示均质圆盘作定轴转动，其中图a）、c）的转动角速度为常数（w=C），而图b）、d）的角速度不为常数（w≠C），则哪个图示圆盘的惯性力系简化的结果为平衡力系？（）
图示均质圆轮，质量为m，半径为r，在铅垂图面内绕通过圆盘中心O的水平轴转动，角速度为w，角加速度为ε，此时将圆轮的惯性力系向O点简化，其惯性力主矢和惯性力主矩的大小分别为：（）
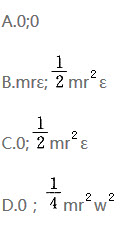
图示机构O1ABO2为一平行四边形，O1A=O2B=R，O1O2=AB=l，在该瞬时杆O1A绕O1轴的角速度为ω，角加速度为ε，则质量为m的均质杆AB的惯性力系向其质心C简化的主矢量R1和主矩的大小分别为（）。
图示均质轮和均质杆，质量均为m；轮子半径均为R，杆长均为l；轮和杆均以角速度ω转动，其中图B中，轮在直线轨道上作纯滚动，则它们的动量大小按图次序为（）。
质量为m，长为2
的均质细杆初始位于水平位置，如图所示。A端脱落后，杆绕轴B转动，当杆转到铅垂位置时，AB杆角加速度的大小为（）。
，则A处约束力大小为（ ）。
题57图
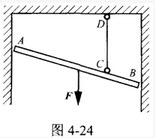
图4-24中，均质杆AB重力为F，用铅垂绳CD吊在天花板上，A、B两端分别靠在光滑的铅垂墙面上，则A、B两端约束力的大小是（）。
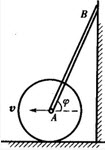
图示平面机构，半径为R的圆轮在水平直线轨道上作纯滚动，图示位置=60°，轮心A的速度为v，杆AB长l，B端紧靠铅直墙，则此瞬时B点速度vB和杆AB的角速度应为（）。
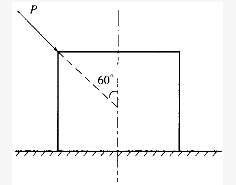
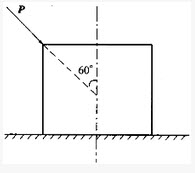
物块重力的大小为5kN，与水平面间的摩擦角为φm=35°。今用与铅垂线成60°角的力P推动物块（如图所示），若P=5kN，则物块是否滑动？（）
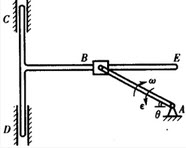
在图示平面机构中，AB杆借助滑套B带动直角杆CDE运动，在图示位置，θ=30°，角速度ω=2rad/s，角加速度ε=1rad/s2，且知曲柄AB长L=10cm，则该瞬时D点的速度V和加速度a为（）。
偏心凸轮机构，偏心距为e，轮半径R=e，轮转动时将推动AB杆绕A轴转动。图示位置，OC⊥CB，OB在铅直位置，此时轮的角速度为ω，杆AB水平，B端搁置缘上，杆长为L，则此瞬时杆AB的角速度应为（）。
质量为m1，半径为r的均质圆盘上，沿水平直径方向焊接一长为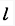
，质量为m2的均质杆AB。整个物体绕圆盘中心O以角速度w转动，该物体系统的总动量的大小为（）。
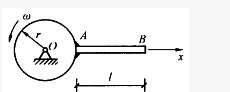
（2011）均质杆AB长为ι，重为W，受到如图所示的约束，绳索ED处于铅垂位置，A、B两处为光滑接触，杆的倾角为α，又CD=ι/4，则A、B两处对杆作用的约束力大小关系为：（）
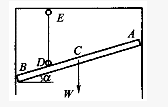
均质细直杆AB长为ι，质量为m，以匀角速度ω绕O轴转动，如图4-69所示，则AB杆的动能为（）。
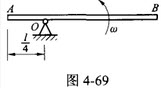
图示均质细杆AB长L，重力的大小为P，与铅垂轴固结成角a=30°，并以匀角速度ω转动，则惯性力系的合力的大小等于（）
图示结构杆①的轴力大小为：（）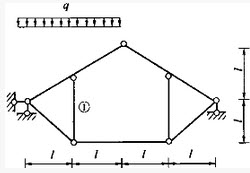
图示结构杆①的轴力大小为：（）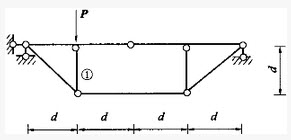
铅垂面的H面投影为直线，有积聚性，且反映（ ）夹角大小。
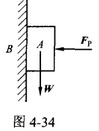
图4-34所示物块A重力的大小W=10N，被用大小为FP=50N的水平力挤压在粗糙的铅垂墙面B上，且处于平衡。块与墙间的摩擦系数f=0.3。A与B间的摩擦力大小为（）。
物块重力的大小为5kN，与水平面间的摩擦角为φn=35°。今用与铅垂线成60°角的力P推动物块（如图所示），若P=5kN，则物块是否滑动？（）
图示杆件AB长2m，B端受一顺时针向的力偶作用，其力偶矩的大小m=100N·m，杆重不计，杆的中点C为光滑支承，支座A的反力FA的大小和方向为：（）
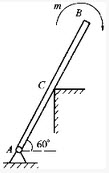
图示杆件AB长2m，B端受一顺时针向的力偶作用，其力偶矩的大小m=100N·m，杆重不计，杆的中点C为光滑支承，支座A的反力FA的大小和方向为：（）
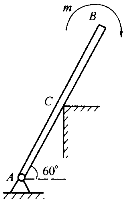
免费的网站请分享给朋友吧