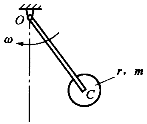
忽略质量的细杆OC=L,其端部固结匀质圆盘。杆上点C为圆盘圆心,盘质量为m,半径为r。系统从角速度ω绕轴O转动,系统的动能是( )。 

 ,其端部固结匀质圆盘。杆上点C为圆盘圆心,盘质量为m,半径为r。系统从角速度ω绕轴O转动,系统的动能是()。
,其端部固结匀质圆盘。杆上点C为圆盘圆心,盘质量为m,半径为r。系统从角速度ω绕轴O转动,系统的动能是()。 






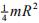 。
。
 ,质量为m2的均质杆AB。整个物体绕圆盘中心O以角速度w转动,该物体系统的总动量的大小为()。
,质量为m2的均质杆AB。整个物体绕圆盘中心O以角速度w转动,该物体系统的总动量的大小为()。 
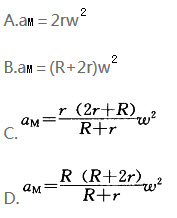
 )时,则圆盘动能T=( )。
)时,则圆盘动能T=( )。



 平动时,则圆盘动能T=( )。
平动时,则圆盘动能T=( )。

 ,半径为r,则圆盘对O轴的动量矩为( )。
,半径为r,则圆盘对O轴的动量矩为( )。
 ,半径为r,则圆盘的动能为( )。
,半径为r,则圆盘的动能为( )。
质量为m1,半径为r的均质圆盘上,沿水平直径方向焊接一长为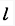 ,质量为m2的均质杆AB。整个物体绕圆盘中心O以角速度w转动,该物体系统的总动量的大小为()。
,质量为m2的均质杆AB。整个物体绕圆盘中心O以角速度w转动,该物体系统的总动量的大小为()。
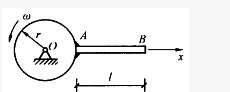
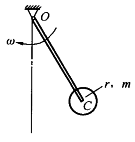
如图4-65所示,忽略质量的细杆OC=ι,其端部固结均质圆盘。杆上点C为圆盘圆心。盘质量为m。半径为r。系统以角速度ω绕轴O转动。系统的动能是()。
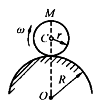
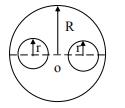
质量为2m,半径为R的偏心圆板可绕通过中心O的轴转动,偏心距OC=R/2。在OC连线上的A点固结一质量为m的质点,OA=R如图示。当板以角速度w绕轴O转动时,系统动量K的大小为()。(注:C为圆板的质心)。

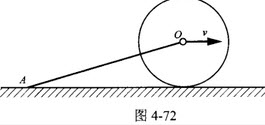
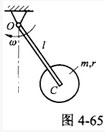
如图4-72所示,质量为m1的均质杆OA,一端铰接在质量为m2的均质圆盘中心,另一端放在水平面上,圆盘在地面上作纯滚动。圆心速度为ν,则系统的动能为()。
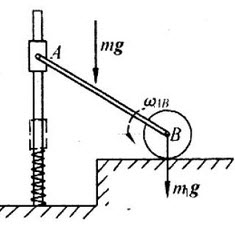
已知均质杆AB的质量m=4kg,长l=600mm,均匀圆盘B的质量为6kg,半径为r=600mm,作纯滚动。弹簧刚度为k=2N/mm,不计套筒A及弹簧的质量。连杆在与水平面成30º角时无初速释放。求(1)当AB杆达水平位置而接触弹簧时,圆盘与连杆的角速度;(2)弹簧的最大压缩量δmax
如图所示,均质圆盘重为W,半径为R,绳子绕过圆盘,两端各挂重为Q和P的物块,绳与盘之间无相对滑动,且不计绳重,则圆盘的角加速度为()。

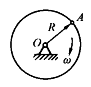
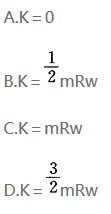
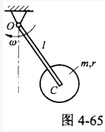
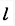 ,其端部固结匀质圆盘。杆上点C为圆盘圆心,盘质量为m,半径为r。系统从角速度ω绕轴O转动,系统的动能是()。
,其端部固结匀质圆盘。杆上点C为圆盘圆心,盘质量为m,半径为r。系统从角速度ω绕轴O转动,系统的动能是()。 
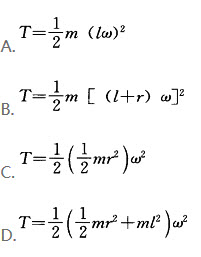
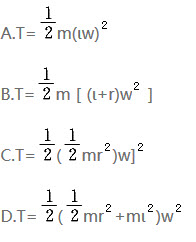
免费的网站请分享给朋友吧