A、<img width="97" height="63" id="图片 2509" src="https://static.tiw.cn//s/tiw/p3/UpLoadImage/2019-11-18/889737b8-08d6-4b99-bf43-fdadb5e5872b.png">
B、<img width="100" height="69" id="图片 2508" src="https://static.tiw.cn//s/tiw/p3/UpLoadImage/2019-11-18/03c9ef62-a160-4b46-84c8-d6fafb93c152.png">
C、<img width="106" height="62" id="图片 2507" src="https://static.tiw.cn//s/tiw/p3/UpLoadImage/2019-11-18/df9e62da-3ce3-4615-a207-25a13d4212ac.png">
D、<img width="99" height="60" id="图片 2506" src="https://static.tiw.cn//s/tiw/p3/UpLoadImage/2019-11-18/ce2fa440-a930-4429-a525-6e76129e47c1.png">
查看答案
正确答案
试题解析
根据题意可知,杆左端的坐标为x=-
l,质点所在处坐标为x=a。在区间[-
l,0]上,取杆上任一小段[x,x+dx],其质量为μdx,其与质点的距离为(a-x),则其与质点间的引力近似为kmμdx/(a-x)
2。故质点与细杆之间引力大小为

。
 。
。
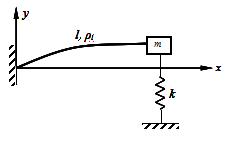
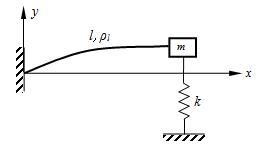

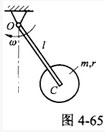
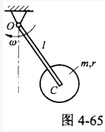
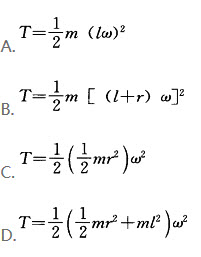
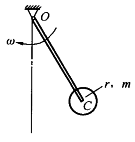
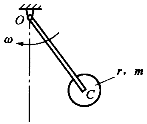
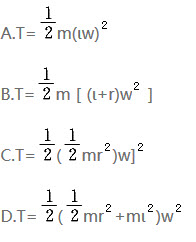
 ,其端部固结匀质圆盘。杆上点C为圆盘圆心,盘质量为m,半径为r。系统从角速度ω绕轴O转动,系统的动能是()。
,其端部固结匀质圆盘。杆上点C为圆盘圆心,盘质量为m,半径为r。系统从角速度ω绕轴O转动,系统的动能是()。 



