矩阵
，已知A有三个线性无关的特征向量，λ＝2是A的二重特征值，可逆矩阵P为（ ），使P－1AP为对角矩阵。
得x＝2，y＝－2。
得λ1＝λ2＝2，λ3＝6。
得ξ3＝（1，－2，3）T。令
则
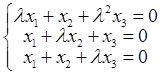的系数矩阵为A，存在方阵B≠0，使得AB＝0。
，则C的伴随矩阵C*=（ ）。
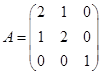，矩阵B满足ABA*＝2BA*＋E，其中A*为A的伴随矩阵，E是单位矩阵，则|B|＝____。
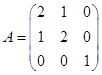，矩阵B满足ABA*＝2BA*＋E，其中A*为A的伴随矩阵，E是单位矩阵，则|B|＝（ ）。
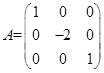，E为单位矩阵，A*为A的伴随矩阵，则B＝（ ）。
可逆，向量α＝（1，b，1）T是矩阵A*的一个特征向量，λ是α对应的特征值，其中A*是矩阵A的伴随矩阵，求非零实数a、b、λ。
____.
，求
的表达式。
设
与
分别代表非齐次线性方程组
的系数矩阵和增广矩阵，若这个方程组无解，则（ ）．
、
、
、
、
中最大的一个是（ ）。
是方程
的一个根，那么分式
的值是（ ）。
，
，…，
是正整数，且
，
＝250，则的最小值为（ ）。
人得优，
人得良，
人及格，其余的均不及格，那么不及格的人数是（ ）。
，
，
，
四个分数按从大到小的顺序排列，第二个数是（ ）。
y＝2x＋3y，x⊙y＝xy，且x、y均为正整数，若当x⊙y＝6时，xy取得最小值，则x等于（ ）。
、
、
、
以上这四个数中，最大的数为最小的数的几倍？（ ）
，
为2阶单位矩阵，矩阵
满足
，则
（ ）。
女，25岁，因眼部外伤来院就诊，CT如图所示，最可能的诊断是（）
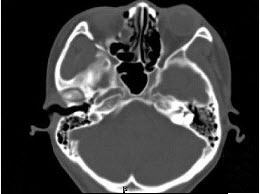
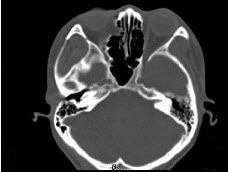
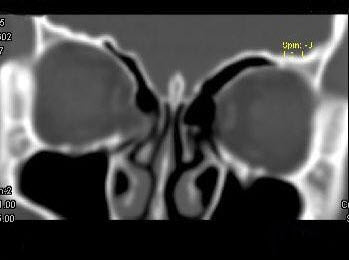
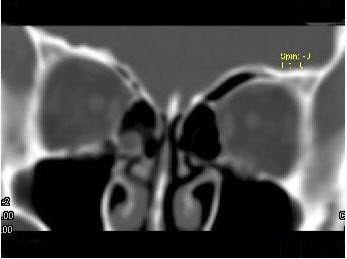
一患者
缺失，
三臂卡，
、
间隙卡环，初戴1周后，诉义齿游离端压痛，咀嚼不适。口腔检查发现，义齿密合，固位稳定良好，咬合无早接触，基托伸展不影响软组织活动，缺隙区黏膜无明显压痛、红肿或溃疡。
患者男性，35岁。
近中中位阻生，
远中颈部可疑龋坏。现拟拔除。
女孩，6岁。右下后牙吃饭时疼痛一周。检查：
龋洞较深，腐质黄褐色，不松动，叩痛（-）。
萌出2/3，近中窝沟微卡探针，略粗糙。
咬合面龋洞浅。
牙色充填体，边缘不密合。
女孩，6岁。右下后牙吃饭时疼痛一周。检查：
龋洞较深，腐质黄褐色，不松动，叩痛（-）。
萌出2/3，近中窝沟微卡探针，略粗糙。
咬合面龋洞浅。
牙色充填体，边缘不密合。
如果腐质没有去尽时牙髓暴露，应进行的治疗步骤是（）。
男，46岁，面部肌肉麻木、疼痛，咀嚼困难，牙痛，MRI检查如图，最可能的诊断是（）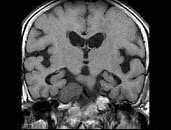
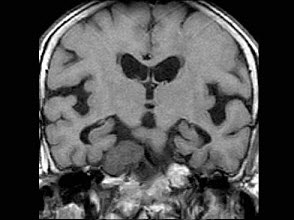
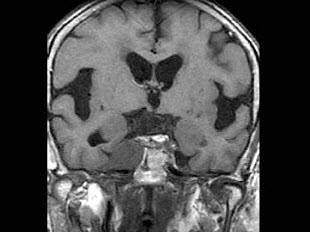
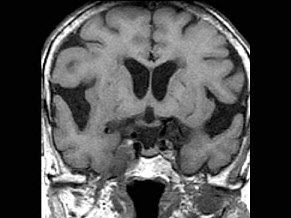
女，45岁，颈强直、发热咳痰2周余，结合CT图像，最可能的诊断是（）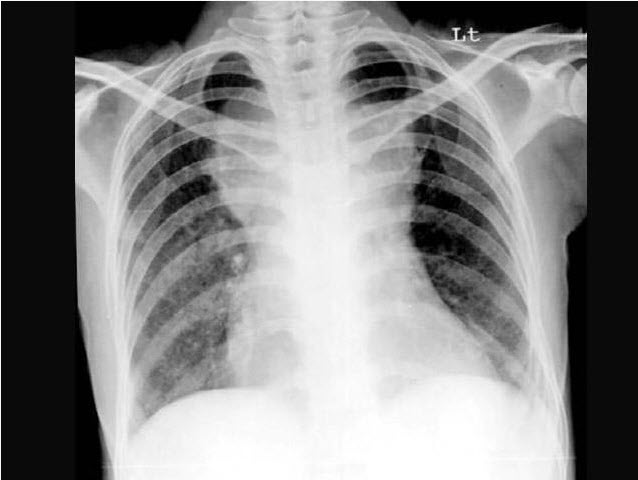
。证明：，已知A有三个线性无关的特征向量，λ＝2是A的二重特征值，可逆矩阵P为（ ），使P－1AP为对角矩阵。
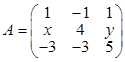，已知A有三个线性无关的特征向量，λ＝2是A的二重特征值，存在可逆矩阵P＝（ ），使P－1AP为对角矩阵。
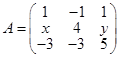，已知A有三个线性无关的特征向量，λ＝2是A的二重特征值，试求出可逆矩阵P，使P－1AP为对角矩阵。
免费的网站请分享给朋友吧