设矩阵
可逆，向量α＝（1，b，1）T是矩阵A*的一个特征向量，λ是α对应的特征值，其中A*是矩阵A的伴随矩阵，求非零实数a、b、λ。
所以有
解得
或
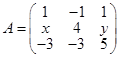，已知A有三个线性无关的特征向量，λ＝2是A的二重特征值，试求出可逆矩阵P，使P－1AP为对角矩阵。
，则C的伴随矩阵C*=（ ）。
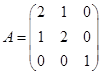，矩阵B满足ABA*＝2BA*＋E，其中A*为A的伴随矩阵，E是单位矩阵，则|B|＝____。
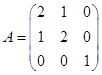，矩阵B满足ABA*＝2BA*＋E，其中A*为A的伴随矩阵，E是单位矩阵，则|B|＝（ ）。
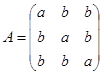若A的伴随矩阵的秩等于1，则必有（ ）.
的每一个方程都表示一个平面，若系数矩阵的秩为3，则三平面的关系是____。
，M∩N＝N，则（ ）．
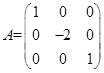，E为单位矩阵，A*为A的伴随矩阵，则B＝（ ）。
可逆，向量α＝（1，b，1）T是矩阵A*的一个特征向量，λ是α对应的特征值，其中A*是矩阵A的伴随矩阵，求非零实数a、b、λ。
，求
的表达式。
设
，则
．（ ）
二阶矩阵
（ ）．
设
为连续型随机变量
的密度函数，则对任意的
，
（ ）．
设
是来自正态总体
的容量为2的样本，其中
为未知参数，则
是的无偏估计．（ ）
用消元法得
的解
为（ ）．
设
是来自正态总体
（
均未知）的样本，则（ ）是统计量．
设是来自正态总体的容量为2的样本，其中为未知参数，则
是的无偏估计．（ ）
设
是随机变量，
，设
，则
（ ）．
设
与
分别代表非齐次线性方程组
的系数矩阵和增广矩阵，若这个方程组有解，则（ ）．
设与分别代表非齐次线性方程组的系数矩阵和增广矩阵，若这个方程组无解，则（ ）．
设
为随机变量，
，当（ ）时，有
．
设连续型随机变量X的密度函数为
，分布函数为
，则对任意的区间
，
（ ）．
设
是来自正态总体
（
均未知）的样本，则统计量（ ）不是
的无偏估计．
设
是矩阵A的属于不同特征值的特征向量，则向量组的秩是（ ）．
二阶矩阵
（ ）．
设线性方程组
的两个解
，则下列向量中（ ）一定是的解.
y＝2x＋3y，x⊙y＝xy，且x、y均为正整数，若当x⊙y＝6时，xy取得最小值，则x等于（ ）。
。证明：
，已知A有三个线性无关的特征向量，λ＝2是A的二重特征值，可逆矩阵P为（ ），使P－1AP为对角矩阵。
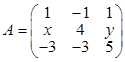，已知A有三个线性无关的特征向量，λ＝2是A的二重特征值，存在可逆矩阵P＝（ ），使P－1AP为对角矩阵。
免费的网站请分享给朋友吧