解：首先，确定目标函数。
设甲、乙两种原料分别用10xg和10yg。病人需要使用的费用为：z=3x+2y。
其次，确定目标函数的可行域（定义域）。
病人每餐至少需要35单位蛋白质，可表示为：5x+7y=；35，
同理，对铁质的要求可以表示为：10x+4y≥40，
这样，问题转变为求目标函数在可行域（由约束条件确定）上的最小值。
或者说，在约束条件下

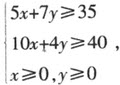
求目标函数z=3x+2y的最小值。
再次，求目标函数在可行域上的最小值。
做出可行域，如所给图示。
令z=0，做直线l₀：3x+2y=0，由图形可知，把直线l₀平移至点A时，z取最小值。
由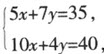得点A的坐标为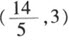，即需甲种原料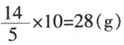，需要乙种原料3×10=30（g）时，费用最省。