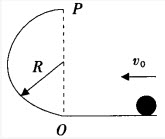
如图所示,小球沿水平面以初速度υ0通过O点进入半径为R的竖直半圆弧轨道,不计一切阻力,下列说法正确的是()
半径为R,质量为m的均质圆盘在其自身平面内作平面运动。在图示位置时,若已知图形上A、B两点的速度方向如图所示。a=45°,且知B点速度大小为vb。则圆轮的动能为()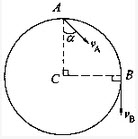
如图所示,物块A重为P,连在不计重量、不伸长的绳子上。绳子绕过定滑轮D并绕在鼓轮B上。当A下落时带动轮C沿水平直线轨道作纯滚动。鼓轮B的半径为r,C的半径为R,两轮固连,总重为Q,其对水平中心轴O的回转半径为ρ,轮D半径r,重不计,则物块A的加速度a为()。
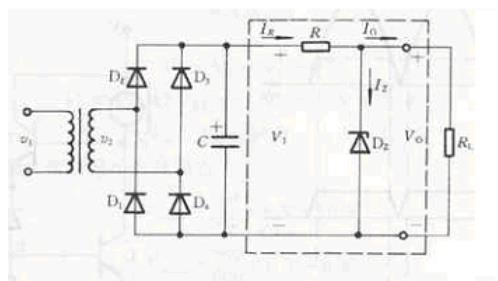 若稳压管Dz的动态电阻r z=20Ω,求稳压电路的内阻R o及面ΔV o/ΔV I的值
若稳压管Dz的动态电阻r z=20Ω,求稳压电路的内阻R o及面ΔV o/ΔV I的值
已知:如图所示平面机构中,曲柄OA=r,以匀角速度ωO转动。套筒A沿BC杆滑动。BC=DE,且BD=CE=l。求图示位置时,杆BD的角速度ω和角加速度α。

 。( )
。( )

半径为R的圆管中,横截面上流速分布为 ,其中r表示到圆管轴线的距离,则在r1=0.2R处的黏性切应力与r2=R处的粘性切应力大小之比为:()
,其中r表示到圆管轴线的距离,则在r1=0.2R处的黏性切应力与r2=R处的粘性切应力大小之比为:()

 v 2的大小
v 2的大小

如图所示,小球沿水平面以初速度υ0通过O点进入半径为R的竖直半圆弧轨道,不计一切阻力,下列说法正确的是()

(b)开路电压UO和等效电阻RO分别为(),()
同心球形电容器,两极的半径分别为R1和R2(R2>R1),中间充满相对介电系数为εr的均匀介质,则两极间场强的分布曲线为下列哪个图所示()?
如图所示,E为内阻不能忽略的电池,R1,RR2,R3,为定值电阻,S0、S为开关,V与A分别为电压表与电流表,初始时S0与S均闭合,现将S断开,则()
一物体以初速度υ0、加速度a做匀加速直线运动,若物体从£时刻起,加速度a逐渐减小至零,则物体从t时刻开始()
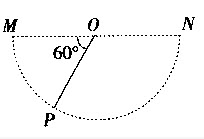
如图所示,M,N和P是以MN为直径的半圆弧上的三点,O点为半圆弧的圆心,∠MOP=60°。电荷量相等、符号相反的两个点电荷分别置于M、N两点,这时O点电场强度的大小为E1;若将N点处的点电荷移至P点,则O点的场场强大小变为E2,E1与E2之比为()
摩天大楼中一部直通高层的客运电梯,行程超过百米.电梯的简化模型如图1所示.考虑安全、舒适、省时等因素,电梯的加速度a是随时间t变化的,已知电梯在t=0时由静止开始上升,a─t图象如图2所示.电梯总质量m=2.0×103kg.忽略一切阻力,重力加速度g取10m/s2.
(1)求电梯在上升过程中受到的最大拉力F1和最小拉力F2;
(2)类比是一种常用的研究方法.对于直线运动,教科书中讲解了由υ─t图象求位移的方法.请你借鉴此方法,对比加速度和速度的定义,根据图2所示a─t图象,求电梯在第1s内的速度改变量△υ1和第2s末的速率υ2;
(3)求电梯以最大速率上升时,拉力做功的功率P;再求在0─11s时间内,拉力和重力对电梯所做的总功W.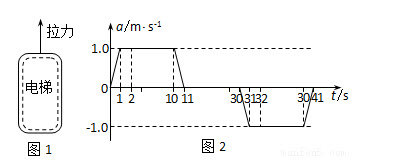
如图所示,质量分别为m1、m2的两个物体通过轻弹簧连接,在力F的作用下一起沿水平方向做匀速直线运动(m1在地面,m2在空中),力F与水平方向成θ角,m1所受支持力N、摩擦力f正确的是()。

质量为m的小球A,在光滑的水平面上以速度υ0。与质量为3m的静止小球B发生正碰,碰撞后A球的速度大小变为原来的1/3,则碰撞后小球B的速度大小可能为()
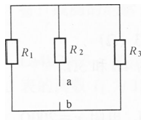
如图D-5所示,已知R1=5Ω、R2=10Ω、R3=20Ω,求电路中a、b两端的等效电阻Rab是多少?
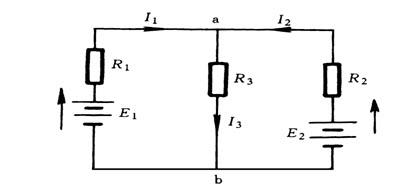
如图所示的电路,利用戴维南定理求支路电流I3。已知E1=140V,E2=90V,R1=20Ω,R2=5Ω,R3=6Ω。
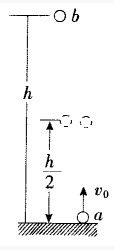
如图所示,将小球a从地面以初速度υ0竖直上抛的同时,将另一相同质量的小球b从距地面^处由静止释放,两球恰在 争处相遇(不计空气阻力),则()。
争处相遇(不计空气阻力),则()。
宇宙飞船在半径为R1的轨道上运行,变轨后的半径为R2,且R1>R2,宇宙飞船绕地球做匀速圆周运动,则变轨后宇宙飞船的()。
复曲线测设时,已知主曲线半径R主为,其切线长为T1,基线长为a,则副曲线半径R副为()。
如图4-2所示.若某平面任意力系满足∑Fx=0,∑Fv=0,且该力系向C点简化的主矩为MC,求该力系向B点简化的结果()。
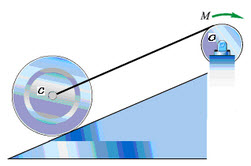
已知:轮O的半径为R1,质量为m1,质量分布在轮缘上;均质轮C的半径为R2,质量为m2,与斜面纯滚动,初始静止。斜面倾角为θ,轮O受到常力偶M驱动。求:轮心C走过路程s时的速度和加速度。
免费的网站请分享给朋友吧