曲线通过(1,1)点,且此曲线在[1,x]上所形成的曲边梯形面积的值等于该曲线终点的横坐标x与纵坐标y之比的二倍减去2,其中x>1,y>0。曲线y=f(x)所满足的微分方程应是:()

设曲线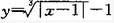 ,则曲线在x=1处存在下述中哪种情况()?
,则曲线在x=1处存在下述中哪种情况()?
由曲线y=x2/2和直线x=1,x=2,y=-1围成的图形,绕直线y=-1旋转所得旋转体体积为:()
已知函数f(x)=x-alnx(a∈R)
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值。
 -ydx+rdy等于()
-ydx+rdy等于()
免费的网站请分享给朋友吧