设函数f(u)在(0,+∞)内二阶可导且![]() 满足等式
满足等式![]() .
.
(1)验证![]() ;
;
(2)若f(1)=0,f′(1)=1,求函数f(u)的表达式。

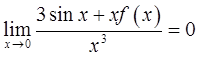 求f(0)、f′(0)、f″(0)。
求f(0)、f′(0)、f″(0)。

设函数f(x)在[0,+∞)上连续,且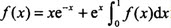 满足,则f(x)是()。
满足,则f(x)是()。
设函数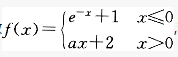 ,若f(x)在x=0处可导,则以的值是:()
,若f(x)在x=0处可导,则以的值是:()
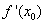 =0,则X。一定是函数的( ).
=0,则X。一定是函数的( ).
设二阶可导函数f(x)>0,若曲线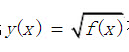 有拐点(1,2),且f′(1)=12,则f″(1)=()。
有拐点(1,2),且f′(1)=12,则f″(1)=()。
免费的网站请分享给朋友吧