有两个二元随机变量X和Y,它们的联合概率为P[X=0,Y=0]=1/8,P[X=0,Y=1]=3/8,P[X=1,Y=1]=1/8,P[X=1,Y=0]=3/8。定义另一随机变量Z=XY,试计算:
(1)H(X),H(Y),H(Z),H(XZ),H(YZ),H(XYZ);
(2)H(X/Y),H(Y/X),H(X/Z),H(Z/X),H(Y/Z),H(Z/Y),H(X/YZ),H(Y/XZ),H(Z/XY);
(3)I(X;Y),I(X;Z),I(Y;Z),I(X;Y/Z),I(Y;Z/X),I(X;Z/Y)。
设函数y=f(x)在点x_0处可导,Δy=f(x_0+h)-f(x_0),则当h→0时,必有( )。

设随机变量X服从参数A=1的指数分布,即X的概率密度函数为
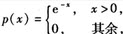
则条件概率P(X>5
X>3)等于().
设F1(x)与F2(x)分别为随机变量X1与X2的分布函数。为使F(x)=aF1(x)-bF2(x)成为某一随机变量的分布函数,则a与b分别是:()
免费的网站请分享给朋友吧