已知函数f(x)可导，则△x→0时， lim [f(x0-x)-f(x0)]/x -题库考试答案搜索网

已知函数f(x)可导，则△x→0时， lim [f(x0-x)-f(x0)]/x

单选题

2021-09-01 16:17

A、-f.(x)
B、f.(-x0)
C、f.(x0)
D、2f.(x0）

查看答案

正确答案

A

试题解析

标签：安徽教育在线合肥财经职业学院计算机网络技术

感兴趣题目

已知X=21，Y=15，Z=22，计算表达式（（X>Y）or（Y>Z））and（（X<><>

设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝____。

设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝（　　）。

设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝（　　）。

设函数f（x）在区间[1，＋∞）内二阶可导，且满足条件f（1）＝f′（1）＝0，x＞1时f″（x）＜0，则g（x）＝f（x）/x在（1，＋∞）内（　　）。

若f（x）是奇函数且f′（0）存在，则x＝0是函数F（x）＝f（x）/x的（　　）。

设函数f（x），g（x）是大于零的可导函数，且f′（x）g（x）-f（x）g′（x）<0，则当a<><>

已知f（x）在x＝a处可导，且f′（a）＝k（k≠0），则____。

设函数y=f(x)在点x_0可导，当自变量由x_0增至x_0+Δx时，记Δy为f(x)的增量，dy为f(x)的微分，则(Δy-dy)/Δx→（　　）（当Δx→0时）。

设函数y=f(x)在点x_0处可导，Δy=f(x_0+h)-f(x_0)，则当h→0时，必有（　　）。

已知f(x)在[a,b]上可导，则f^' (x)<0是f(x)在[a,b]上单减的（　　）。

设y=f(x)有反函数，x=g(y)，且y_0=f(x_0)，已知f^' (x_0)=1，f^('_0^' )，则g^('_0^' )（　　）。

相关题目: 已知函数y=f（x）对一切x满足，若f’（x0）=0（x0≠0），则（）．; 已知函数f(x)可导，则△x→0时， lim [f(x0-x)-f(x0)]/x; 设函数可导y=f(x),且f(xo)≠0,则当x∆→0时,函数f(x)在xo处的微分dy是( ); 已知f.(x0)=0,则可导函数y=f(x)在点x0处（）; 设函数f(x)=｛(e√∣x∣-1)0,1/sinx,x≠0,x=0则x=0是函数f(x)的( ); 设f(x)在[0,+∞)上有二阶导数,f(0)=0,f(x)在[0,+∞)上为单调减函数,则函数g(x)=f(x)/x在(0,+∞)上为( ).; 若函数 f ( x ) 在点 x 0 处可导, 则 limf（xo-h）-f(x0）/h=（）; 已知函数f(x)=exx≤0 x+kx≥0在点x=0 处连续，则k=; 设函数f(x)在区间[0,1]上连续，在开区间(0,1)内可导，且f＇(x)＞0,则( ); 已知可导y=f(x)可导，则∫f′(x)dx（）; 若y=f(x)在(∞,+∞)内二阶可导,且f(-x)=f(x)当x>0时,f(x)>0,f(x)<0则<0时,有(); 若f(x)在区间1上可导，且f(x)=0，x∈i，则f在区间i上是常函数．（）; ( x ) 设f(x)在0,a上二阶可导,且xf(x)-f(x)>0则F(x)/x 在(0,a)内是(); 已知函数f(x)=x(x-1)(x-2)(x-3),则方程f(x)=0有 ___ 个实根。; 已知函数在x₀处可导，且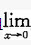｛x／[f（x₀-2x）-f（x₀）]｝=1／4，则f′（x₀）的值为：（）; 设可导函数f（x）满足xf′（x）-f（x）＞0，则（）。; 已知x=10，表达式“x＞10 And x＜=100 Or 10 Mod 2=0"的值为( )。; 已知函数f（x）的定义域为[0，4]，则函数φ（x）＝f（x＋1）＋f（x－1）的定义域为____。; 已知函数f(x)的定义域为[0，4]，则函数φ(x)=f(x+1)+f(x-1)的定义域为____.; 设函数f（x），g（x）二次可导，满足函数方程f（x）g（x）＝1，又f′（x）≠0，g′（x）≠0，则f″（x）/f′（x）－f′（x）/f（x）＝g″（x）/g′（x）－g′（x）/g（x）。

广告位招租WX:84302438

题库考试答案搜索网

免费的网站请分享给朋友吧