设三阶方阵A、B满足A2B-A-B=E,其中E为三阶单位矩阵。若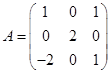 求行列式|B|的值。
求行列式|B|的值。
 所以知A+E可逆。
所以知A+E可逆。 故,B,=,(A-E)-1,=(,A-E,)-1=1/2。
故,B,=,(A-E)-1,=(,A-E,)-1=1/2。 ,则B=( )。
,则B=( )。
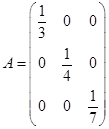 ,则B=( )。
,则B=( )。
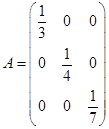 则B=____。
则B=____。
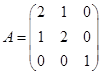 ,矩阵B满足ABA*=2BA*+E,其中A*为A的伴随矩阵,E是单位矩阵,则|B|=____。
,矩阵B满足ABA*=2BA*+E,其中A*为A的伴随矩阵,E是单位矩阵,则|B|=____。
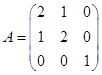 ,矩阵B满足ABA*=2BA*+E,其中A*为A的伴随矩阵,E是单位矩阵,则|B|=( )。
,矩阵B满足ABA*=2BA*+E,其中A*为A的伴随矩阵,E是单位矩阵,则|B|=( )。
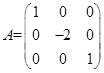 ,E为单位矩阵,A*为A的伴随矩阵,则B=( )。
,E为单位矩阵,A*为A的伴随矩阵,则B=( )。
 E为单位矩阵,A*为A的伴随矩阵,则B=____。
E为单位矩阵,A*为A的伴随矩阵,则B=____。

设a,b,c是任意的非零平面向量,且相互不共线,有以下结论
①(a·b)·c-(c·a)·b=0;
②|a|-|b|<|a-b|;
③(b·c)·a-(c·a)·b不与c垂直;
④(3a+2b)(3a-2b)=9|a|2-4|b|2,
其中正确的是()。
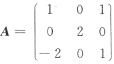 ,求行列式|B|的值。
,求行列式|B|的值。
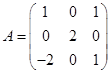 求行列式|B|的值。
求行列式|B|的值。
免费的网站请分享给朋友吧