A、<img src='/s/tiw/p3/UpLoadImage/2017-11-22/cf6e1a70-3a1c-47e2-943c-5c8b904421b1.jpg' title='a.jpg' width='143' height='30' border='0' hspace='0' vspace='0' style='float:none;width:143px;height:30px;'>
B、<img src='/s/tiw/p3/UpLoadImage/2017-11-22/ccf7dd30-1d98-4be3-bd96-b431ab9abd12.jpg' title='b.jpg' width='153' height='30' border='0' hspace='0' vspace='0' style='float:none;width:153px;height:30px;'>
C、<img src='/s/tiw/p3/UpLoadImage/2017-11-22/5a7d91c3-f604-402c-b8f0-ce5f219d504c.jpg' title='c.jpg' width='128' height='30' border='0' hspace='0' vspace='0' style='float:none;width:128px;height:30px;'>
D、<img src='/s/tiw/p3/UpLoadImage/2017-11-22/093303e9-33e0-45f1-aa00-bc30924fa2aa.jpg' title='d.jpg' width='132' height='30' border='0' hspace='0' vspace='0' style='float:none;width:132px;height:30px;'>
查看答案
正确答案
试题解析
因为AB＝0，所以r（A）＋r（B）≤3，又A≠0，B≠0，所以1≤r（A）＜3，1≤r（B）＜3，故|B|＝0。又因为λ＝-2时，
即此时r（A）=3。事实上，当λ=1时，r（A）=1符合要求。故当λ＝-2时不符合题意。
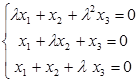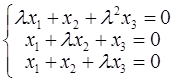的系数矩阵为A，存在方阵B≠0，使得AB=0.
的系数矩阵为A，存在方阵B≠0，使得AB＝0。
的系数矩阵为A，存在方阵B≠0，使得AB＝0。
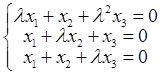的系数矩阵为A，存在方阵B≠0，使得AB＝0。
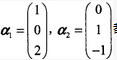，都是齐次线性方程组Ax=0的解，则矩阵A为（）。
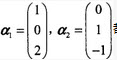，都是齐次线性方程组Ax=0的解，则矩阵A为（）。