n阶矩阵A的伴随矩阵为A*,齐次线性方程组AX=O有两个线性无关的解,则( ).
A、A<sup>*</sup>X=0的解均是AX=0的解
B、AX=0的解均是A<sup>*</sup>X=O的解
C、AX=0与A<sup>*</sup>X=0无非零公共解
D、AX=0与A<sup>*</sup>X=O仅有2个非零公共解
查看答案
正确答案
试题解析
由齐次方程组AX=0有两个线性无关的解向量,知方程组AX=0的基础解系所含解向量的个数为n-r(A)≥2,即r(A)≤n-2<n-1.由矩阵A与其伴随矩阵秩的关系,知r(A*)=0,即A*=0.所以任意n维列向量均是方程组A*X=0的解,故方程组AX=0的解均是A*X=0的解.

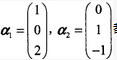 ,都是齐次线性方程组Ax=0的解,则矩阵A为()。
,都是齐次线性方程组Ax=0的解,则矩阵A为()。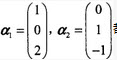 ,都是齐次线性方程组Ax=0的解,则矩阵A为()。
,都是齐次线性方程组Ax=0的解,则矩阵A为()。