设f(x)在(-∞,+∞)内可导,则( )。
设函数f(x)=x|x|,x∈(-∞,+∞),则( )。
设函数y=f(x)在点x_0处可导,Δy=f(x_0+h)-f(x_0),则当h→0时,必有( )。
已知f(x)在(-∞,+∞)上可导,则( )。
若f(x)在x_0处可导,则|f(x)|在x_0处( )。
设f(x)在(-∞,+∞)内可导,则( )。
设周期函数f(x)在(-∞,+∞)内可导,周期为3,又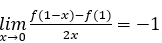 ,则曲线在点(4,f(4))处的切线斜率为( )。
,则曲线在点(4,f(4))处的切线斜率为( )。
已知f(x)在[a,b]上可导,则f^' (x)<0是f(x)在[a,b]上单减的( )。
设f(x)=√(1-e^(-x^2 ) ),则( )。
若f(x)是可导的,以C为周期的周期函数,则f'(x) =( )。
设f(x)=g(a+bx)-g(a-bx),其中g(x)在(-∞,+∞)有定义,且在x=a可导,则f^' (0) =( )。
设y=f(cosx)·cos( f(x)),且f可导,则y^'=( )。

设f(x)在积分区间上连续,则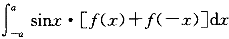 等于:()
等于:()
设f(x)在(-∞,+∞)二阶可导,f′(x0)=0。问f(x)还要满足以下哪个条件,则f(x0)必是f(x)的最大值()?
设函数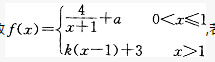 ,若,f(x)在点x=1处连续而且可导,则k的值是:()
,若,f(x)在点x=1处连续而且可导,则k的值是:()
设二阶可导函数f(x)>0,若曲线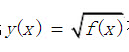 有拐点(1,2),且f′(1)=12,则f″(1)=()。
有拐点(1,2),且f′(1)=12,则f″(1)=()。
设f(x)在积分区间上连续,则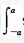 sinx?[f(x)+f(-x)]dx等于:()
sinx?[f(x)+f(-x)]dx等于:()
免费的网站请分享给朋友吧