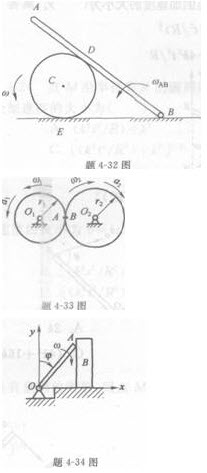
杆OA=ι,绕定轴O以角速度ω转动,同时通过A端推动滑块B沿轴x运动(见图)。设分析运动的时间内杆与滑块并不脱离,则滑块的速度υB的大小用杆的转角ψ与角速度ω表示为()。
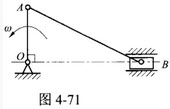


已知:如图所示平面机构中,曲柄OA=r,以匀角速度ωO转动。套筒A沿BC杆滑动。BC=DE,且BD=CE=l。求图示位置时,杆BD的角速度ω和角加速度α。

曲柄机构在其连杆AB的中点C与CD杆铰接,而CD杆又与DE杆铰接,DE杆可绕E点转动。曲柄OA以角速度w=8rad/s绕O点逆时针向转动。且OA=25cm,DE=100cm。在图示瞬时,O、A、B三点共在一水平线上,B、E两点在同一铅直线上,∠CDE=90°,则此时DE杆角速度的大小和方向为:()

(2008)杠OA=ι,绕定轴O以角速度w转动,同时通过A端推动滑块B沿轴X运动,设分析运动的时间内杆与滑块并不脱离,则滑块的速度vB的大小用杆的转角φ与角速度w表示为:()
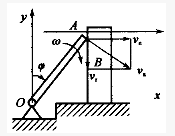
杆OA=ι,绕定轴O以角速度ω转动,同时通过A端推动滑块B沿轴x运动(图4-49)。设分析运动的时间内杆与滑块并不脱离,则滑块的速度νB的大小用杆的转角φ与角速度ω表示为()。

在定平面O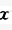
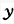 内,杆OA可绕轴O转动,杆AB在点A与杆OA铰接,即杆AB可绕点A转动。该系统称为双摆,其自由度数为:()
内,杆OA可绕轴O转动,杆AB在点A与杆OA铰接,即杆AB可绕点A转动。该系统称为双摆,其自由度数为:()
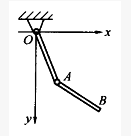
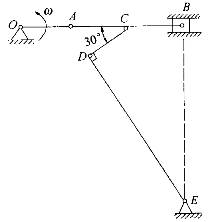
如图4-71所示曲柄连杆机构中,OA=r,AB=2r,OA、AB及滑块B质量均为m,曲柄以ω的角速度绕O轴转动,则此时系统的动能为()。
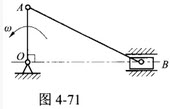
科氏加速度)如图所示平面机构,AB长为l,滑块A可沿摇杆OC的长槽滑动。摇杆OC以匀角速度ω绕轴O转动,滑块B以匀速ν═lω沿水平导轨滑动。图示瞬时OC铅直,AB与水平线OB夹角为30º。求:此瞬时AB杆的角速度及角加速度。
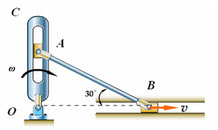

 图4-2-13
图4-2-13
 图4-2-17
图4-2-17
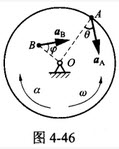
如图4-46所示,圆盘某瞬时以角速度ω,角加速度α绕轴O转动,其上A、B两点的加速度分别为αA和αB,与半径的夹角分别为θ和φ。若OA=R,OB=R/2,则αA和αB,θ与φ勺关系分别为()。
杆OA=ι,绕定轴O以角速度ω转动,同时通过A端推动滑块B沿轴x运动(见图)。设分析运动的时间内杆与滑块并不脱离,则滑块的速度υB的大小用杆的转角ψ与角速度ω表示为()。

偏心凸轮机构,偏心距为e,轮半径R=e,轮转动时将推动AB杆绕A轴转动。图示位置,OC⊥CB,OB在铅直位置,此时轮的角速度为ω,杆AB水平,B端搁置缘上,杆长为L,则此瞬时杆AB的角速度应为()。

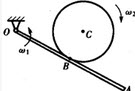
图示杆OA以角速度ψ1绕O轴旋转,轮C相对杆以角速度ω2在杆上滚动。轮半径为R,杆长为2l,此瞬时OB=BA。若以轮心C为动点,动系固结在OA杆上,则C点的牵连速度vE为()。
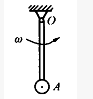
质量为m,长度为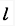 的均质杆铰接于O点,A端固结一质量为m的质点如图示。当OA杆以角速度w绕O轴转动时,系统对轴O的动量矩的大小为()。
的均质杆铰接于O点,A端固结一质量为m的质点如图示。当OA杆以角速度w绕O轴转动时,系统对轴O的动量矩的大小为()。
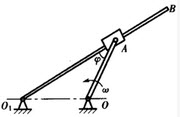
图示平面机构,曲柄OA长R,以角速度ω绕O轴转动,并通过杆端滑块A带动摆杆O1B绕O1轴转动。已知OA=OO1,图示位置=300,则此时杆O1B的角速度为()。
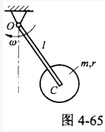
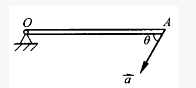
杆OA绕固定轴O转动,长为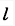 。某瞬时杆端A点的加速度为
。某瞬时杆端A点的加速度为 ,如图所示。则该瞬时OA杆的角速度及角加速度为()。
,如图所示。则该瞬时OA杆的角速度及角加速度为()。

免费的网站请分享给朋友吧