A、α<sub>1</sub>+α<sub>2</sub>,α<sub>2</sub>+α<sub>3</sub>,α<sub>3</sub>-α<sub>1</sub>
B、α<sub>1</sub>+α<sub>2</sub>,α<sub>2</sub>+α<sub>3</sub>,α<sub>1</sub>+2α<sub>2</sub>+α<sub>3</sub>
C、α<sub>1</sub>+2α<sub>2</sub>,2α<sub>2</sub>+3α<sub>3</sub>,3α<sub>3</sub>+α<sub>1</sub>
D、α<sub>1</sub>+α<sub>2</sub>+α<sub>3</sub>,2α<sub>1</sub>-3α<sub>2</sub>+22α<sub>3</sub>,3α<sub>1</sub>+5α<sub>2</sub>-5α<sub>3</sub>
查看答案
正确答案
试题解析
[解析] 解法1:设k
1(α
1+2α
2)+k
2(2α
2+3α
3)+k
3(3α3+α
1)=0
即(k
1+k
3)α
1+(2k
1+2k
2)α
2+(3k
2+3k
3)α
3=0
由α
1、α
2、α
3线性无关得
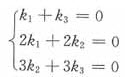
其系数行列式为
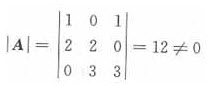
故上述方程组有唯一零解,即k
1=k
2=k
3=0
故α
1+2α
2,2α
2+3α
3,3α
3+α
1线性无关。
解法2:(用排除法):
①由于α
3-α
1=(α
2+α
3)-(α
1+α
2),即A中向量组线性相关,排除选项A;
②由于α
1+2α
2+α
3=(α
1+α
2)+(α
2+α
3),B中向量组线性相关,可排除选项B;
③对于D,由于
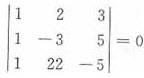
,故方程组AX=0存在非零解,
即向导组α
1+α
2+α
3,2α
1-3α
2+22α
3,3α
1+5α
2-5α
3线性相关,排除D;故正确答案为C。
