A是三阶矩阵，A，A+E，E-2A均不可逆，则矩阵A的三个特征值是（）。 -题库考试答案搜索网

A是三阶矩阵，A，A+E，E-2A均不可逆，则矩阵A的三个特征值是（）。

单选题

2022-01-10 01:08

A、0，1，2
B、0，-1，2
C、0，-1，<img src="http://imgcdn.ehafo.com/ppkaoImg/a17f6ceff0b2457001b6d45b2a5eb101">
D、0，-1，<img src="http://imgcdn.ehafo.com/ppkaoImg/ecd38319fcc06ee28dfb7fd0355b9fec">

查看答案

正确答案

试题解析

[解析] 按定义，若|λE-A|=0，则λ是A的特征值。因为矩阵A，A+E，E-2A均不可逆，故
|0E-A|=(-1)³|A|=0
|-E-A|=(-1)³|A+E|=0

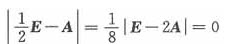
于是矩阵A的特征值为0，-1，

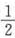
，故正确答案为C。

标签：在职攻读硕士联考

感兴趣题目

设x1、x2是三阶矩阵A的属于特征值λ1的两个线性无关的特征向量，x3是A的属于特征值λ2的特征向量，且λ1≠λ2，则（）。

设A是三阶矩阵，α1=（1，0，1）T，α2=（1，1，0）T是A的属于特征值1的特征向量，α3=（0，1，2）T是A的属于特征值-1的特征向量，则：（）

A是三阶矩阵，A，A+E，E-2A均不可逆，则矩阵A的三个特征值是（）。

已知A、B为三阶矩阵，且有相同的特征值1，2，2，则下列命题：①A，B等价；②A，B相似；③若A，B为实对称矩阵，则A，B合同；④行列式|A-2E|=|2E-A|，成立的有

已知A是n阶可逆矩阵，那么与A有相同特征值的矩阵是（　　）。

已知n阶可逆矩阵A的特征值为λ0，则矩阵（2A）-1的特征值是（　　）。[2012年真题]

已知n阶可逆矩阵A的特征值为λ0，则矩阵（2A）－1的特征值是（　　）。[2012年真题]

设A为三阶矩阵，有特征值为1，-1，2，则下列矩阵中可逆矩阵是（）。

设A为可逆矩阵，则与A必有相同特征值的矩阵为________。

设矩阵A，X为同阶方阵，且A可逆，若A(X-E)=E，则矩阵X=________。