设n阶矩阵A＝（aij），其中，求A的特征值与特征向量。 -题库考试答案搜索网

设n阶矩阵A＝（a_ij），其中，求A的特征值与特征向量。

问答题

2022-06-18 15:38

查看答案

正确答案

由题可知矩阵

则其特征值行列式为

解得λ₁=a+(n-1)b,λ₂=λ₃=…=λ_n=a-b。
当λ₁=a+(n-1)b时,因

所以矩阵A的属于特征值λ₁=a+(n-1)b的全部特征向量为k₁ξ(→)₁=k₁(1,1,…,1)^T(k₁≠0)。
当λ₂=λ₃=…=λ_n=a-b时,特征值多项式组成的方程组和方程组x₁+x₂+x₃+…+x_n=0同解,其基础解系为n-1个n维列向量,ξ(→)₂=(-1,1,0,…,0)^T,ξ(→)₃=(-1,0,1,0,…,0)^T,…,ξ(→)_n=(-1,0,0,…,1)^T,所以属于矩阵A的特征值λ₂=λ₃=…=λ_n=a-b的全部特征向量为k₂ξ₂+k₃ξ₃+…+k_nξ_n,k₂,k₃,…,k_n不同时为0。

试题解析

标签：考研公共课数学

感兴趣题目

设A是m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r，矩阵B＝AC的秩为r1，则（　　）。

设数列｛a_n｝前n项和为S_n，且a_n+S_n=1（n∈N^*）
（1）求｛a_n｝的通项公式；
（2）若数列｛b_n｝满足b₁=1且2b_n+1=b_n+a_n（n≥1），求数列｛b_n｝的通项公式。

设A为n阶方阵，A*是A的伴随矩阵，则||A|A*|等于（　　）.

设A，N，A+B，A-1+B-1均为n阶可逆矩阵，则（A-1+B-1）=（）。

设a₁和b₁都大于0，a_n=（a_n-1+b_n-1）/2，b_n=2a_n-1b_n-1/（2a_n-1+b_n-1），则a_n和b_n的极限分别为（）（sqrt和inf分别表示根号和无穷）

设方程组

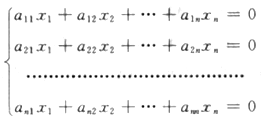的系数行列式|A|=0，而|A|中的某个元素a_ij的代数余子式A_ij≠0.

设行列式

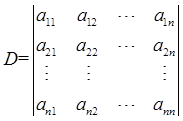中的元素都是实数，而且至少有一个不为0，若a_ij＝A_ij（A_ij是a_ij的代数余子式），证明Dⁿ^－²＝1。

对于矩阵连乘所需最少数乘次数问题，其递归关系式为：

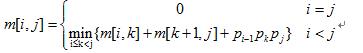其中m[i，j]为计算矩阵连乘Ai…Aj所需的最少数乘次数，p _i-1为矩阵Ai的行，Pi为矩阵Ai的列。现有四个矩阵，其中各矩阵维数分别为：

请根据以上的递归关系，计算出矩阵连乘积A ₁A ₂A ₃A ₄所需要的最少数乘次数。

设A为n阶方阵，A*是A的伴随矩阵，则||A|A*|等于（　　）。

设A为n阶方阵，A*是A的伴随矩阵，则||A|A*|等于（　　）。

设n阶矩阵A＝（a_ij），其中

，求A的特征值与特征向量。

已知a₁=3且a_n=S_n-1+2ⁿ，求a_n及A_N。

相关题目: 设A为m×n矩阵,B为n×m矩阵,m≠n, 则下列矩阵中为n阶矩阵的是( )。; 设A为n阶对称矩阵,B为n阶反对称矩阵,则下列矩阵中为反对称矩阵的是( ); 设A实n阶矩阵，且A的行列式∣A∣=0，则A中; 设 n阶矩阵A的行列式 , 是的伴随矩阵,则( ); 级数前几项和s_n=a₁+a₂+…+a_n，若a_n≥0，判断数列｛s_n｝有界是级数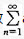a_n收敛的什么条件（）？; 设A为n阶可逆矩阵，则（-A）的伴随矩阵（-A）*等于（）。; 设A是m阶矩阵，B是n阶矩阵，行列式等于（）。; 设A为n阶矩阵，且满足等式A2=A，E为n阶单位矩阵，则下列结论正确的是; 设A为n阶实对称矩阵，B为n阶可逆矩阵，Q为n阶正交矩阵，则下列矩阵与A有相同特征值的是; 设n阶矩阵A有n个两两正交的特征向量，证明A是对称矩阵。; 设n阶矩阵A有n个两两正交的特征向量，证明A是对称矩阵.; 设A为n阶方阵，E为n阶单位矩阵，且A2=A，则（A-2E）-1=____.; 设A为n阶矩阵，A经过若干次初等变换后得到矩阵B，则; 设A是n阶对称矩阵，B是n阶反对称矩阵，则下列不能用正交变换化为对角矩阵的是; 设T=（t1，t2，„„，tn）为概率向量，P=（P_ij）_n*n为概率矩阵，则当k→∞时，必有（）; 设A是n阶方阵，AAT=E，|A|＜0，求|A+E|，其中AT是A的转置矩阵.; 设A是n阶方阵，AAT＝E，|A|＜0，求|A＋E|，其中AT是A的转置矩阵。; 设A是m阶矩阵，B是n阶矩阵，行列式等于（）。; 设A是m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r，矩阵B＝AC的秩为r1，则（　　）。; 设A是m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r，矩阵B=AC的秩为r1，则（　　）.

广告位招租WX:84302438

题库考试答案搜索网

免费的网站请分享给朋友吧